filmov
tv
Number Theory | Euler's Totient Function and Powers of Primes

Показать описание
We give a formula for the value of Euler's totient function on powers of primes.
Euler’s Totient Function (Phi Function)
Euler's totient function | Journey into cryptography | Computer Science | Khan Academy
Number Theory | The Multiplicativity of Euler's Totient Function
Euler’s Totient Function (Solved Examples)
Euler's Phi Function
Introduction to Euler's Totient Function!
Last 2 digits using Euler's Totient Function
Number Theory | Euler's Totient Function and Powers of Primes
Number Theory 34: Euler totient function
Euler's Totient Theorem and Fermat's Little Theorem - Complete Proof & Intuition
Euler's phi function |Solved examples |Cryptography
Euler's Totient Function Number Theory 13
Euler totient function made easy
Euler's Theorem
Euler's Toitient Function in Cryptography and Network Security
Euler's theorem numerical examples | Important for exams
Number Theory | Euler's Theorem Example 1
Number Theory 11 10 Euler Totient Function Introduction
Explicit Formula for Euler's Totient Function!
Euler Zn(θ)=e^(θ+17n)i +e^(2.5θ+17n)i
Number Theory 35: Euler totient function evaluation
Euler's Toient Function Explained with Examples in Hindi
Number Theory 11 10 Euler Totient Function Formula for Totient Function of a prime
Number Theory: Euler Theorem
Комментарии
 0:08:40
0:08:40
 0:02:18
0:02:18
 0:13:18
0:13:18
 0:12:53
0:12:53
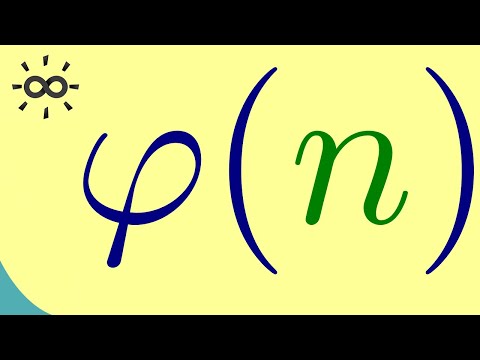 0:03:28
0:03:28
 0:06:56
0:06:56
 0:17:15
0:17:15
 0:08:39
0:08:39
 0:03:47
0:03:47
 0:15:29
0:15:29
 0:10:38
0:10:38
 0:35:28
0:35:28
 0:07:22
0:07:22
 0:08:14
0:08:14
 0:07:42
0:07:42
 0:06:54
0:06:54
 0:05:05
0:05:05
 0:05:52
0:05:52
 0:07:05
0:07:05
 0:00:11
0:00:11
 0:04:13
0:04:13
 0:08:26
0:08:26
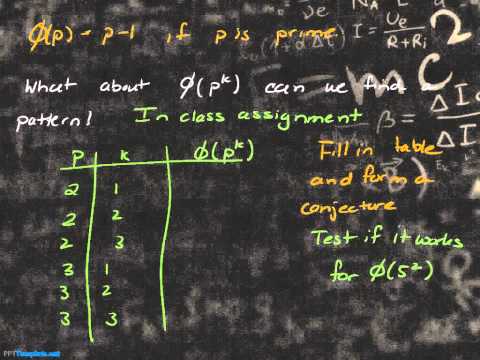 0:03:09
0:03:09
 0:06:24
0:06:24