Recent progress in K-stability of Fano varieties II, Ziquan Zhuang

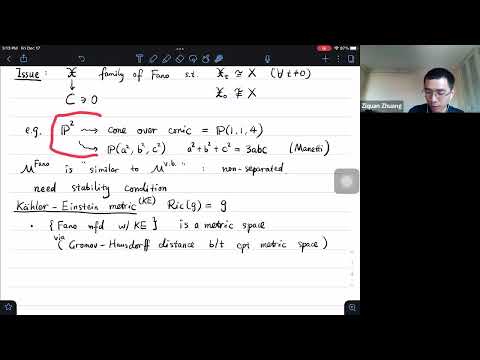
K-stability was first introduced by Tian to characterize the solution of the Kähler-Einstein problem on Fano varieties. In the last decade, a purely algebraic geometric study of K-stability has prospered, based on the birational classification theory of varieties centered around the minimal model program. In the first part of this lecture series, we will discuss algebraic geometer's gradually evolving understanding of the K-stability through birational geometry and valuation theory. We will introduce the higher rank finite generation (HRFG) conjecture, and explain its connection to several foundational questions in K-stability. In the second part, we will discuss our recent joint work with Chenyang Xu, on settling the finite generation conjecture.

This is part of the special month on singularities and K-stability in May/June 2021.