Laplace Transform Second Shifting Theorem Example

preview_player
Показать описание
Let u5(t)=u(t-5) be the unit step function with jump discontinuity at t=5. The differential equation IVP dy/dt + 6y = u5(t), y(0)=4 is best solved by using the Laplace Transform. We also need the so-called Second Shifting Theorem (Property), a.k.a. shifting on the t-axis property, as well as other properties of the Laplace Transform. The differential equation gets converted to an algebraic equation before the Inverse Laplace Transform and Shifting Theorem are used. The Second Shifting Theorem says that ℒ[u(t-a)f(t-a)]=e^(-a*s)F(s). This means the Inverse Laplace Transform of e^(-a*s)F(s) is u(t-a)f(t-a).

Links and resources
===============================

AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
  1. Bill Kinney
  2. laplace transform
  3. laplace transform second shifting theorem
  4. laplace transform second shifting theorem problems
  5. unit step function laplace transform
  6. unit step function
Рекомендации по теме
Laplace Transform: Second 0:08:19

Laplace Transform: Second Shifting Theorem

Laplace Transform Second 0:11:29

Laplace Transform Second Shifting Theorem Example

Second shifting theorem: 0:10:31

Second shifting theorem: Laplace transforms

Second shifting theorem 0:10:38

Second shifting theorem of Laplace transforms

Laplace Transform | 0:12:31

Laplace Transform | Second Shifting Theorem | Concept & Example by GP Sir

Second Shifting Theorem 0:11:28

Second Shifting Theorem (Problems ) | Laplace Transforms (Part 14)| S2(2019) | S4(MA 202) | KTU

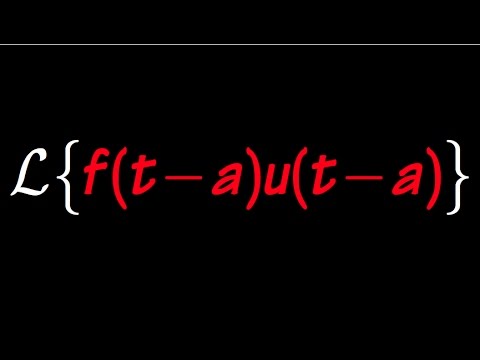Laplace Transform of 0:06:27

Laplace Transform of a Piecewise Function (Unit Step Function)

Laplace Transform. Second 0:15:40

Laplace Transform. Second Translation Theorem.

Second shifting theorem: 0:39:32

Second shifting theorem: Laplace transforms

Second Shifting Theorem 0:09:36

Second Shifting Theorem | Inverse Laplace Transform | BSc 5th Semester | Mathematics 7 B | AP Degree

Second Shifting Theorem 0:07:48

Second Shifting Theorem | Type 1 Problems | t Shift | Heaviside Theorem | Laplace transform | Maths

Laplace & Inverse 0:10:06

Laplace & Inverse Laplace Transform - Second Shifting Theorem | GP Sir

Laplace transform of 0:12:16

Laplace transform of f(t-a)u(t-a), the shifted unit step function

Laplace Transform: First 0:35:14

Laplace Transform: First and Second Shifting Theorem

Second Shiting Theorem 0:10:20

Second Shiting Theorem | Laplace Transform | BSc 5th Semester | Mathematics - 7 B | AP Degree |

Second shifting function 0:01:01

Second shifting function Laplace transform

Inverse Laplace transform 0:11:42

Inverse Laplace transform of Second Shifting Theorem in English

JNTU B.Tech M1 0:10:20

JNTU B.Tech M1 Maths. Second Shifting Theorem Statement and Proof on Laplace Transforms

Second Shifting Theorem 0:18:06

Second Shifting Theorem /Laplace Transforms/Video-5

2nd shift Theorem 0:05:22

2nd shift Theorem Inverse Laplace Transform Example 2

Laplace Transform - 0:17:47

Laplace Transform - Second Shifting Theorem

##state and proof 0:09:09

##state and proof second shifting theorem Laplace transformation

LAPLACE TRANSFORMS SECOND 0:09:35

LAPLACE TRANSFORMS SECOND SHIFTING THEOREM IN TELUGU

Second Shifting Property 0:10:37

Second Shifting Property in Laplace Transform | Second Shifting Theorem | Examples and Solutions