filmov
tv
Find the limit of (1/sinx - 1/tanx) as x approaches 0 WITHOUT L'Hopitals Rule!
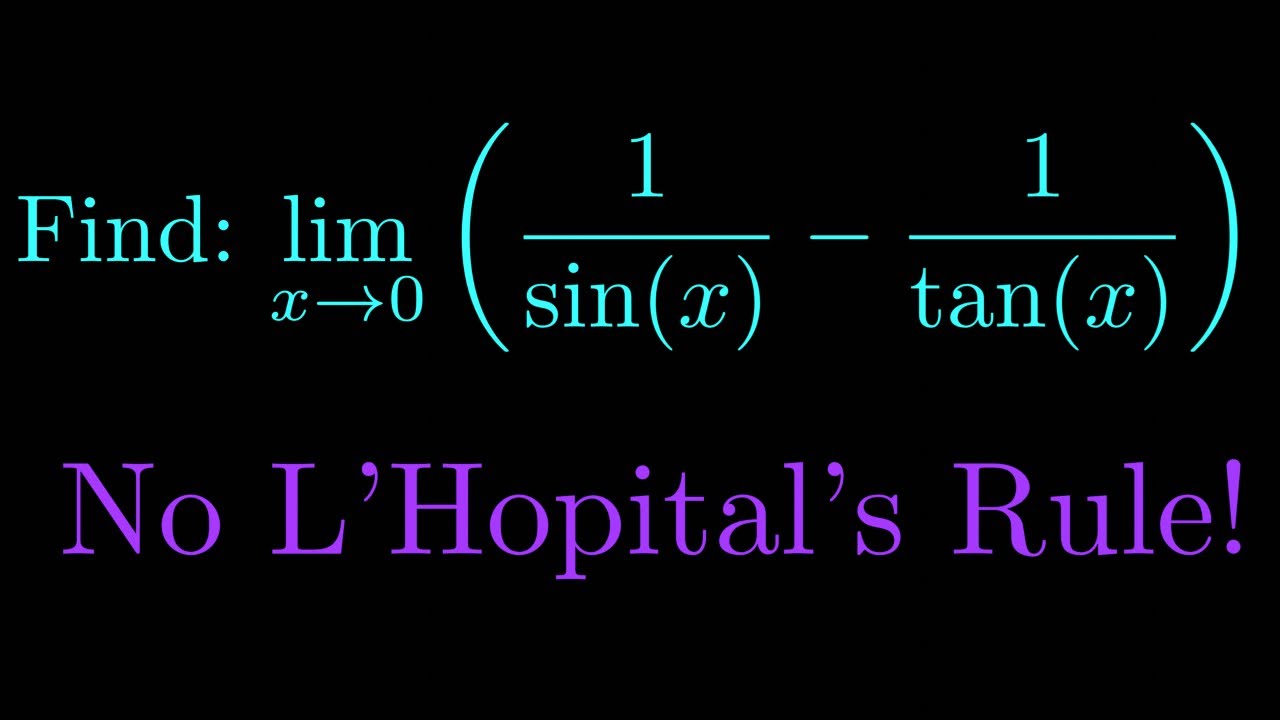
Показать описание
In this video we find the limit of of (1/sinx - 1/tanx) as x approaches 0 without using L'Hopital's rule. Each step is explained carefully. Limit laws, trig identities etc are all taken for granted in this problem.
If you found this content useful, make sure to SUBSCRIBE and check out some of my other videos! Thanks for watching I hope you have a great day. All questions are welcome.
I have linked some videos below which I think you may find useful! If you are struggling on this topic make sure to check them out!
Limit of x^x^x as x goes to 0+ :
Limit of (1+1/x)^x as x approaches infinity :
Limit of (x/x+a)^x as x approaches infinity :
Limit of x^x as x goes to 0+ :
I hope you have a great day!
If you found this content useful, make sure to SUBSCRIBE and check out some of my other videos! Thanks for watching I hope you have a great day. All questions are welcome.
I have linked some videos below which I think you may find useful! If you are struggling on this topic make sure to check them out!
Limit of x^x^x as x goes to 0+ :
Limit of (1+1/x)^x as x approaches infinity :
Limit of (x/x+a)^x as x approaches infinity :
Limit of x^x as x goes to 0+ :
I hope you have a great day!
Use Infinite Series To Find the Limit of (1/sin(x) - 1/x) as x approaches zero
Limit of (1/x - 1/sin(x)) as x approaches zero
Find the limit of (1/sinx - 1/tanx) as x approaches 0 WITHOUT L'Hopitals Rule!
Find the limit using L’Hopital’s Rule as x approaches 0 for (1/x - 1/sin x).
Limit of (1 - sin(x))/(1 + cos(2x)) as x approaches pi/2 with L'Hopital's Rule
Find the limit as x approaches pi/2 for (1- sin x)/(1 + cos 2x). l’Hospitals’ Rule
Find the limit as x approaches 0 for (e^(2x) -1)/(sin x)
Limits Using Sinx/x =1
Calculus II ep34: Taylor series (Dec 3, 2024)
lim x/ Sinx as x tends to 0 , # trick # Easy # Short
Limit[x-(pi/2)+ of cosx/(1-sinx)
Proving a Limit of sin(x)/x
Limits of Trigonometric Functions
Find limit as x approaches (pi/2)^+ for cos x/(1 - sin x) l’Hospitals’ Rule
Find the Limit of sec(x)/(1 - sin(x)) as x approaches 0
Finding Limits using Limit of Sin(x)/x = 1: Tangent Example | Limits | Calculus | Glass of Numbers
Find the limit as x approaches pi/2 for (1- sin x)/(csc x). Use l’Hospitals’ Rule when appropriate...
limit (1-tanx)/(sinx-cosx) as x approaches pi/4
Find the limits. lim_x →0 e^x-1/sinx
`lim_(x- gtpi/2){(1-sinx)tanx}`
Limit of sin(1/x) as x approaches 0 Does Not Exist | Calculus 1 Exercises
Limit of (cos x - 1)/sin x ❖ Calculus 1 ❖ Trig Limits
lim [sin(x)(1-cosx))/x^2, trig limit example(watch to end to see all work in one place)
lim x approaches 0: (1-cosx)/(sinx)
Комментарии
 0:04:34
0:04:34
 0:04:41
0:04:41
 0:02:47
0:02:47
 0:03:19
0:03:19
 0:06:04
0:06:04
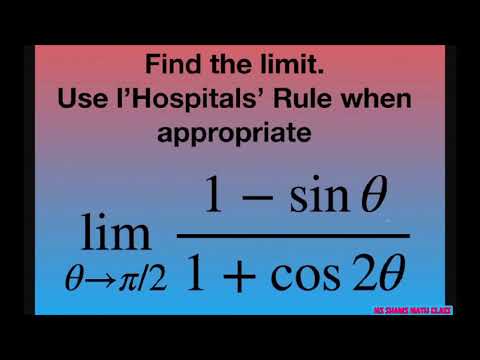 0:02:59
0:02:59
 0:03:10
0:03:10
 0:05:55
0:05:55
 1:11:50
1:11:50
 0:00:17
0:00:17
 0:07:30
0:07:30
 0:01:00
0:01:00
 0:15:23
0:15:23
 0:02:46
0:02:46
 0:01:37
0:01:37
 0:11:49
0:11:49
 0:02:08
0:02:08
 0:01:49
0:01:49
 0:00:33
0:00:33
 0:02:12
0:02:12
 0:04:36
0:04:36
 0:03:08
0:03:08
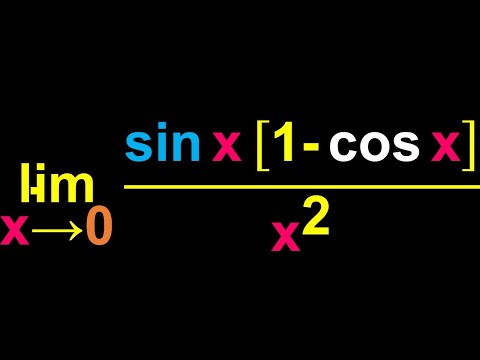 0:01:01
0:01:01
 0:06:10
0:06:10