Ternary search in 4 min python

### ternary search tutorial

#### what is ternary search?

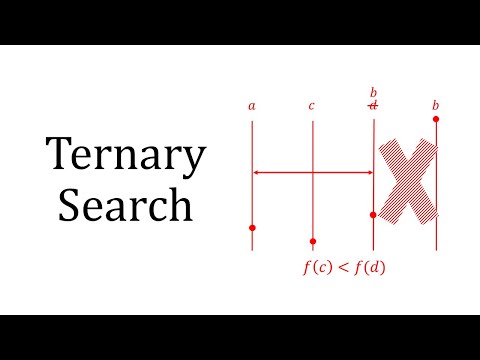
ternary search is a divide-and-conquer search algorithm that is used to find the maximum or minimum of a unimodal function. unlike binary search, which divides the search space into two parts, ternary search splits the array into three parts. this algorithm is efficient for unimodal functions and works best on sorted arrays.

#### characteristics of ternary search

1. **unimodal function**: it works only on unimodal functions where there is a single peak or trough.
2. **time complexity**: the time complexity of ternary search is \(o(\log_3 n)\), which is better than linear search but not as good as binary search in practice.
3. **space complexity**: \(o(1)\) for iterative implementation and \(o(\log n)\) for recursive implementation due to stack space.

#### how ternary search works

1. **divide**: split the array into three parts using two midpoints.
2. **conquer**: compare the midpoints with the target element.
3. **narrow down**: depending on the comparisons, eliminate one or two-thirds of the search space and continue searching in the remaining part.

#### ternary search algorithm

here’s how to implement a ternary search in python:

### explanation of the code

1. **function definition**: the function `ternary_search` takes an array `arr`, and indices `left` and `right` which represent the current search space, along with the `target` value.

2. **base condition**: the function checks if the `right` index is greater than or equal to the `left` index to ensure the search space is valid.

3. **midpoint calculation**: two midpoints (`mid1` and `mid2`) are calculated to divide the search space into three parts.

4. **comparison**: the function checks if the `target` is equal to either midpoint. if found, it returns the index.

5. **recursive calls**: based on the comparisons:
- if the target is less than the first midpoint, search the left segment.
- if the target is greater than the second midpoi ...

#python min key
#python min index
#python min int
#python min max
#python min

python min key
python min index
python min int
python min max
python min
python min function
python minimize
python min of list
python min heap
python minecraft
python search and replace string
python search engine
python search algorithms
python search string
python search array for value
python search string for substring
python search list for string
python search for file in directory