filmov
tv
L22.1 Laplace equation with azimuthal symmetry
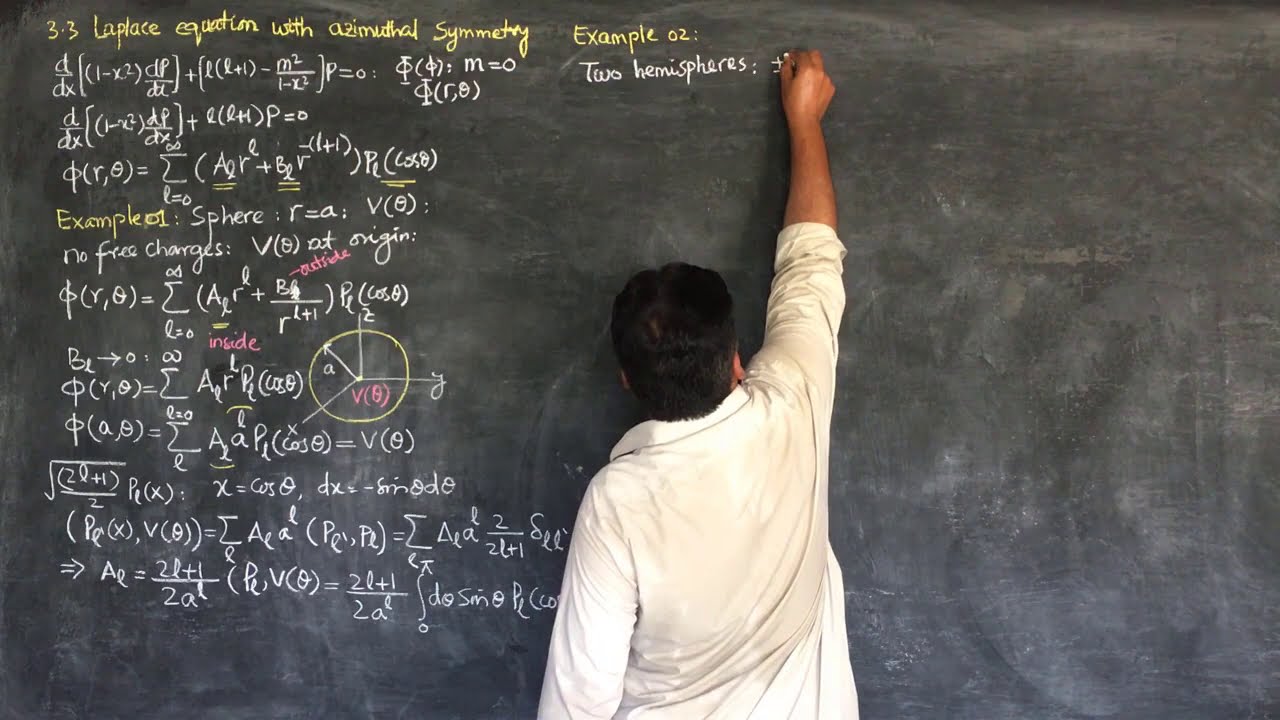
Показать описание
#Laplaceequationinsphericalcoordinates #classicalelectrodynamics #jdjackson
Laplace equation, azimuthal symmetry, boundary value problems, classical electrodynamics, Jackson
Classical Electrodynamics, Third Edition, by John David Jackson, John Wiley and Sons, (1998).
From Wikipedia, the free encyclopedia
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties.
This is called Poisson's equation, a generalization of Laplace's equation. Laplace's equation and Poisson's equation are the simplest examples of elliptic partial differential equations.
Laplace’s equation is also a special case of the Helmholtz equation.
The general theory of solutions to Laplace's equation is known as potential theory. The solutions of Laplace's equation are the harmonic functions,[1] which are important in branches of physics, notably electrostatics, gravitation, and fluid dynamics. In the study of heat conduction, the Laplace equation is the steady-state heat equation.
In this chapter the discussion of boundary-value problems is continued. Spherical and cylindrical geometries are first considered, and solutions of the Laplace equation are represented by expansions in series of the appropriate orthonormal functions.
Only an outline is given of the solution of the various ordinary differential equations obtained from the Laplace equation by separation of variables, but the properties of the different functions are summarized.
The problem of construction of Green functions in terms of orthonormal functions arises naturally in the attempt to solve the Poisson equation in the various geometries. Explicit examples of Green functions are obtained and applied to specific problems, and the equivalence of the various approaches to potential problems is discussed.
Laplace equation, azimuthal symmetry, boundary value problems, classical electrodynamics, Jackson
Classical Electrodynamics, Third Edition, by John David Jackson, John Wiley and Sons, (1998).
From Wikipedia, the free encyclopedia
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties.
This is called Poisson's equation, a generalization of Laplace's equation. Laplace's equation and Poisson's equation are the simplest examples of elliptic partial differential equations.
Laplace’s equation is also a special case of the Helmholtz equation.
The general theory of solutions to Laplace's equation is known as potential theory. The solutions of Laplace's equation are the harmonic functions,[1] which are important in branches of physics, notably electrostatics, gravitation, and fluid dynamics. In the study of heat conduction, the Laplace equation is the steady-state heat equation.
In this chapter the discussion of boundary-value problems is continued. Spherical and cylindrical geometries are first considered, and solutions of the Laplace equation are represented by expansions in series of the appropriate orthonormal functions.
Only an outline is given of the solution of the various ordinary differential equations obtained from the Laplace equation by separation of variables, but the properties of the different functions are summarized.
The problem of construction of Green functions in terms of orthonormal functions arises naturally in the attempt to solve the Poisson equation in the various geometries. Explicit examples of Green functions are obtained and applied to specific problems, and the equivalence of the various approaches to potential problems is discussed.
Комментарии
 0:17:01
0:17:01
 0:17:01
0:17:01
 0:17:00
0:17:00
 0:19:25
0:19:25
 0:16:57
0:16:57
 0:22:00
0:22:00
 0:43:49
0:43:49
 0:16:55
0:16:55
 0:16:21
0:16:21
 1:38:32
1:38:32
 0:16:44
0:16:44
 0:15:08
0:15:08
 0:44:00
0:44:00
 0:32:26
0:32:26
 0:09:52
0:09:52
 0:11:57
0:11:57
 0:00:11
0:00:11
 0:15:35
0:15:35
 0:22:01
0:22:01
 0:13:54
0:13:54
 1:10:40
1:10:40
 0:15:45
0:15:45
 0:34:35
0:34:35
 1:07:32
1:07:32