filmov
tv
Integral of ∫tan^4(x)dx using the Reduction Formula

Показать описание
In this video, we work through the process of solving the integral of ∫tan^4(x)dx with the reduction formula we derived in an earlier video.
The idea with the reduction formula is to reduce the power to lower powers until we can use the standard integral for tan^2(x).
Remember tan^4(x) = [tan(x)]^4.
We also find the integral for a more general case: ∫tan^4(ax)dx by applying a simple substitution and the reduction formula
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
The idea with the reduction formula is to reduce the power to lower powers until we can use the standard integral for tan^2(x).
Remember tan^4(x) = [tan(x)]^4.
We also find the integral for a more general case: ∫tan^4(ax)dx by applying a simple substitution and the reduction formula
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
Integral of tan^4x
Class 12th – Integral of Tan^4x dx | Integrals | Tutorials Point
Integral of tan^4x
Integration Super Method for tan 4 power x | tan^4 x Integration | @Kamaldheeriya Maths easy
integral of tan^4x*sec^6x, calculus 2 tutorial
Integration of tan^4 x sec^4 x
Class 12th – Integral of Tan^8 x Sec^4 x dx | Integrals | Tutorials Point
157. Integral de tangente a la cuarta. TRIGONOMETRICA. EJERCICIO RESUELTO.
Multivariate Calculus Tutorial 6 - Parametrization and Line Integrals
integral of tan^2x*sec^4x, calculus 2 tutorial
Integral of tan^3x*sec^4x (read pinned comment)
Integral of sec^4(x)tan^2(x)dx #maths #calculus #integral #usubstitution #mathproblems
Integral of sec^4(x)tan^2(x)dx
How REAL Men Integrate Functions
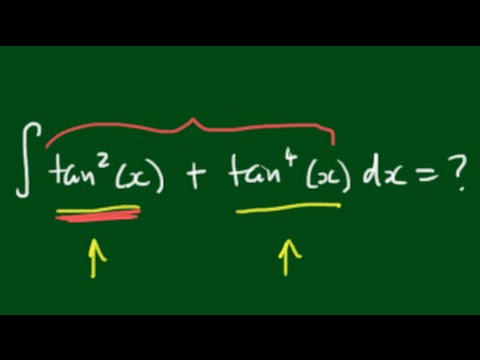
Evaluating the integral ∫tan^2(x)+tan^4(x)dx
when calculus students use trig identities too early
Evaluate ∫0^(π/4) x tan^2 x dx | Integral calculus Problem | Tamil
Integral of tan^5(x)
Evaluate the Integral from 0 to pi/3 of tan^5 x sec^4 x dx. U-Substitution. Example 23
Integral of tan^3(x)
Reduction Formula for Integral of ∫tan^n(x)dx
Integral of tan(x)
Tamasha Dekho 😂 IITian Rocks Relatives Shock 😂😂😂 #JEEShorts #JEE #Shorts
Calculus Integration Strategy Trig tan^6x sec^4x Even Power Products
Комментарии
 0:04:09
0:04:09
 0:02:49
0:02:49
 0:03:09
0:03:09
 0:04:01
0:04:01
 0:04:54
0:04:54
 0:02:50
0:02:50
 0:04:05
0:04:05
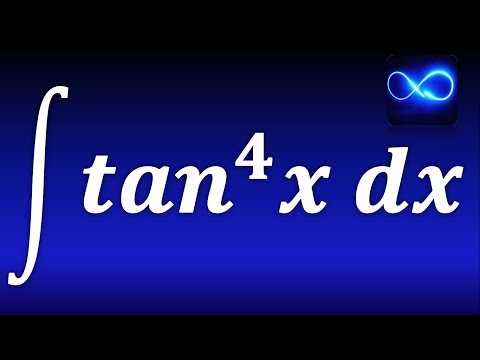 0:04:53
0:04:53
 1:07:06
1:07:06
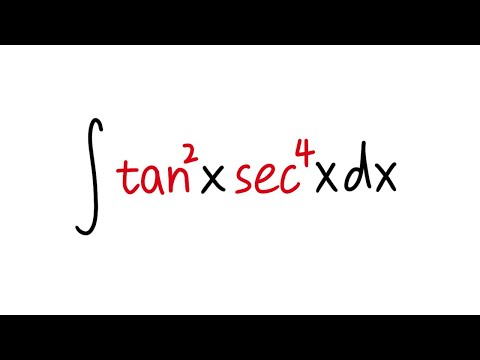 0:07:38
0:07:38
 0:04:17
0:04:17
 0:00:52
0:00:52
 0:03:34
0:03:34
 0:00:35
0:00:35
 0:02:46
0:02:46
 0:00:43
0:00:43
 0:07:52
0:07:52
 0:06:43
0:06:43
 0:04:30
0:04:30
 0:06:03
0:06:03
 0:04:57
0:04:57
 0:02:54
0:02:54
 0:00:13
0:00:13
 0:05:30
0:05:30