filmov
tv
Derivative of ln(3x) with Chain Rule | Calculus 1 Exercises

Показать описание
We differentiate ln(3x) using the chain rule. The outside function f(x) is f(x) = lnx, and the inside function g(x) is g(x)=3x. Then, f(g(x)) = ln(3x), so we see we've identified the outside and inside functions correctly. Applying the chain rule, we have the derivative of f(g(x)) is f'(g(x))*g'(x) = 1/x. #calculus1 #apcalculus
◉Textbooks I Like◉
★DONATE★
Thanks to Loke Tan, Matt Venia, Micheline, Doug Walker, Odd Hultberg, Marc, Roslyn Goddard, Shlome Ashkenazi, Barbora Sharrock, Mohamad Nossier, Rolf Waefler, Shadow Master, and James Mead for their generous support on Patreon!
Outro music is mine. You cannot find it anywhere, for now.
Follow Wrath of Math on...
◉Textbooks I Like◉
★DONATE★
Thanks to Loke Tan, Matt Venia, Micheline, Doug Walker, Odd Hultberg, Marc, Roslyn Goddard, Shlome Ashkenazi, Barbora Sharrock, Mohamad Nossier, Rolf Waefler, Shadow Master, and James Mead for their generous support on Patreon!
Outro music is mine. You cannot find it anywhere, for now.
Follow Wrath of Math on...
Derivative of ln(3x) with Chain Rule | Calculus 1 Exercises
How to Find the Derivative of f(x) = ln(x^3 + 1) using the Chain Rule
Chain rule with natural log: derivative of ln(x^2-3x+5). #shorts
Take the derivative of the natural log function
How to Differentiate y=ln(lnx) using the Chain Rule
Derivative of ln(3x-sinx)
Differentiate y=ln(ln(3x^3))
Differentiation - e and ln
Find the derivative of ln(x^3+3x^2)^5
Chain Rule: d/dx ln(3x^2 - x)
More Chain Rule (NancyPi)
Implicit differentiation with the chain rule and in
Can You Solve This Calculus 1 Derivative? - ln(3x)
Finding the Derivative of f(x) = ln(ln(lnx)) using the Chain Rule
find the derivative of ln(3x-2)
How to find derivative of y=ln(3x^2+5x+7) l How to solve?
Derivative of ln(3x) 5(x)
Derivative of Logarithmic Functions
Derivative of (ln(4x) * (3x^2))
Find y' if y = ln(3x^(2) + 5y^(2)).
Chain Rule For Finding Derivatives
Derivative of y=ln(x^2+3x) using Chain Rule #basics #maths #concepts #2024 #differentiation
Derivatives of Exponential Functions
Ex 2: Derivatives of the Natural Log Function with the Chain Rule
Комментарии
 0:01:58
0:01:58
 0:01:16
0:01:16
 0:00:29
0:00:29
 0:00:43
0:00:43
 0:01:33
0:01:33
 0:00:35
0:00:35
 0:03:25
0:03:25
 0:13:00
0:13:00
 0:01:41
0:01:41
 0:00:28
0:00:28
 0:11:56
0:11:56
 0:05:25
0:05:25
 0:00:52
0:00:52
 0:01:25
0:01:25
 0:00:33
0:00:33
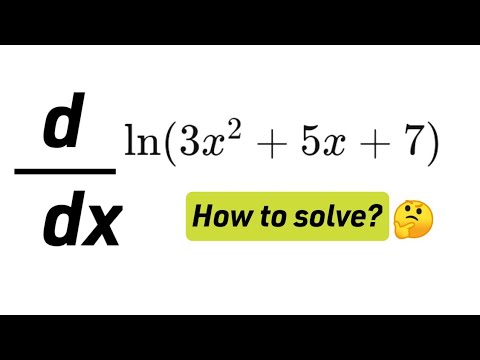 0:01:53
0:01:53
 0:01:38
0:01:38
 0:12:13
0:12:13
 0:02:22
0:02:22
 0:03:00
0:03:00
 0:18:40
0:18:40
 0:00:58
0:00:58
 0:12:03
0:12:03
 0:02:25
0:02:25