filmov
tv
How to Solve the ambiguous case
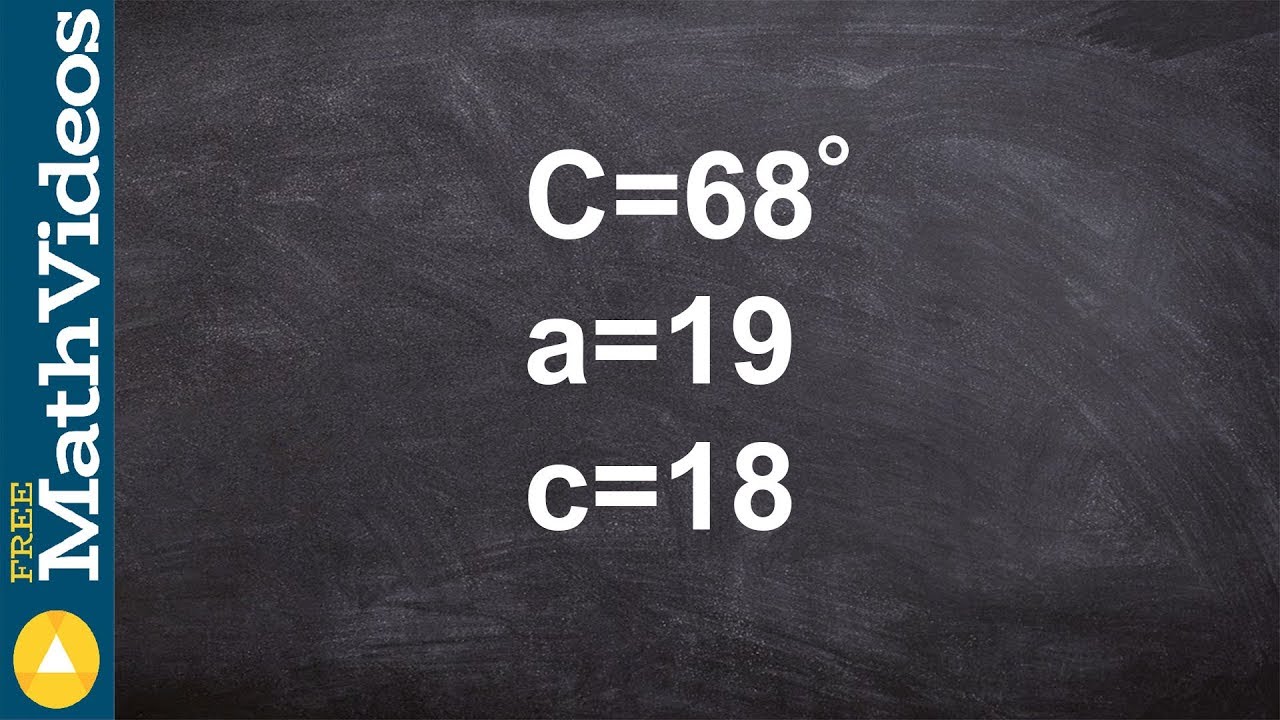
Показать описание
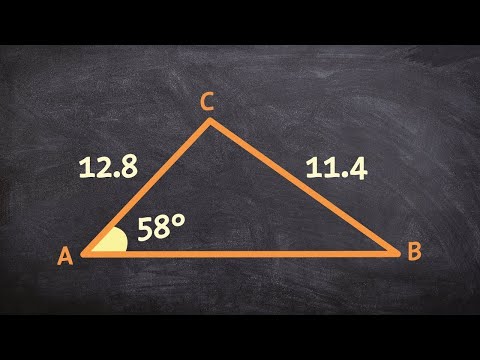
👉 Learn how to determine if a given SSA triangle has 1, 2 or no possible triangles. Given two adjacent side lengths and an angle opposite one of them (SSA or ASS), then there are 3 possible cases: there can be 1 solution, 2 solutions, and no solution.
Using the law of sines, we can obtain the value of the angle opposite the second given side length.
Case 1: If the product of the sine of the given angle and the given side adjacent to the given angle is greater than the given side opposite the given angle, then there is no possible solution satisfying the given values.
Case 2: If the obtained angle is greater than the given angle, then there are 2 possible solutions satisfying the given values.
Case 3: If the obtained angle is less than the given angle, then there is only 1 possible solution satisfying the given values.
Organized Videos:
✅ Law of Sines
✅ Determine 1, 2 or No Triangle
✅ Law of Sines | Learn About
✅ Law of Sines | ASA
✅ Law of Sines | AAS
✅ Law of Sines Ambiguous Case 2 Triangles
✅ Law of Sines Ambiguous Case 1 Triangle
✅ Law of Sines Ambiguous Case No Triangle
✅ Ambiguous Case Law of Sines | Learn About
✅ Find the Area of an Oblique Triangle SAS
Connect with me:
#analytictrig #brianmlogan
Using the law of sines, we can obtain the value of the angle opposite the second given side length.
Case 1: If the product of the sine of the given angle and the given side adjacent to the given angle is greater than the given side opposite the given angle, then there is no possible solution satisfying the given values.
Case 2: If the obtained angle is greater than the given angle, then there are 2 possible solutions satisfying the given values.
Case 3: If the obtained angle is less than the given angle, then there is only 1 possible solution satisfying the given values.
Organized Videos:
✅ Law of Sines
✅ Determine 1, 2 or No Triangle
✅ Law of Sines | Learn About
✅ Law of Sines | ASA
✅ Law of Sines | AAS
✅ Law of Sines Ambiguous Case 2 Triangles
✅ Law of Sines Ambiguous Case 1 Triangle
✅ Law of Sines Ambiguous Case No Triangle
✅ Ambiguous Case Law of Sines | Learn About
✅ Find the Area of an Oblique Triangle SAS
Connect with me:
#analytictrig #brianmlogan
Комментарии
 0:07:23
0:07:23
 0:05:46
0:05:46
 0:15:58
0:15:58
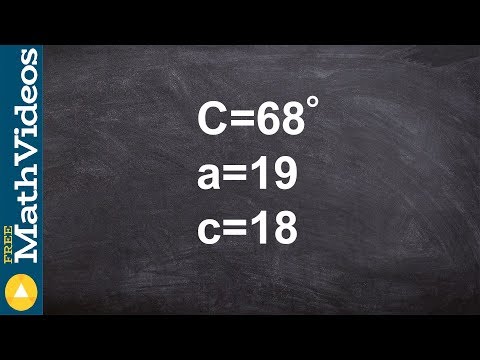 0:15:20
0:15:20
 0:02:22
0:02:22
 0:05:44
0:05:44
 0:13:43
0:13:43
 0:03:05
0:03:05
 1:41:54
1:41:54
 0:08:23
0:08:23
 0:00:42
0:00:42
 0:05:24
0:05:24
 0:15:29
0:15:29
 0:04:27
0:04:27
 0:02:46
0:02:46
 0:00:59
0:00:59
 0:12:22
0:12:22
 0:21:12
0:21:12
 0:17:08
0:17:08
 0:08:22
0:08:22
 0:04:50
0:04:50
 0:07:58
0:07:58
 0:15:02
0:15:02
 0:03:25
0:03:25