filmov
tv
Deriving the Spherical Laplacian (Shortcut Method) w/ Bonus Polar, Cylindrical
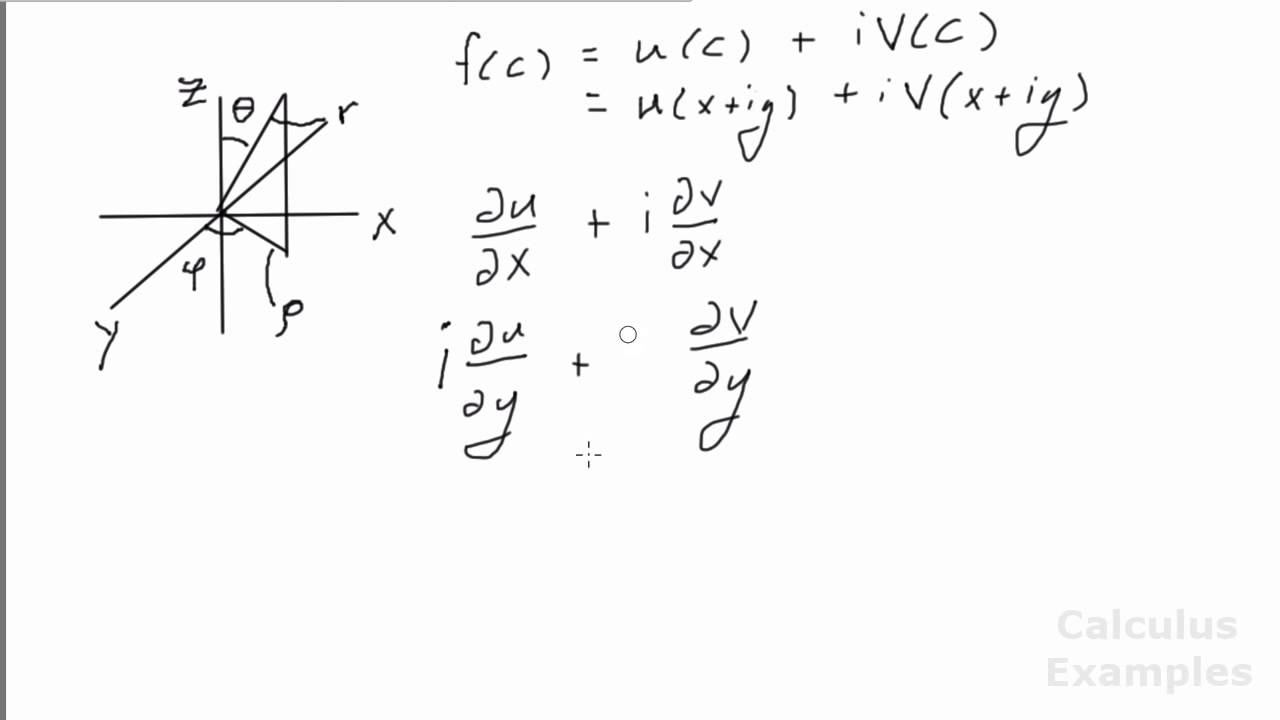
Показать описание
Here we derive the spherical laplacian using complex variables to eliminate the mountains of work that would normally be required.
Useful on examinations.
Also useful for those who can never remember the spherical laplacian and want a short method to derive it.
Useful on examinations.
Also useful for those who can never remember the spherical laplacian and want a short method to derive it.
Deriving the Spherical Laplacian (Shortcut Method) w/ Bonus Polar, Cylindrical
Derive the Laplacian for a Spherical Coordinate System in 4 Steps
Deriving the spherical form of Laplace equation
How to derive the spherical Laplace operator?
Converting the Laplacian to Spherical Coords
Laplacian intuition
Differential forms calculation: the Laplacian in spherical, cylindrical coords (Part 1)
Deriving the polar form of 2D Laplacian
The 3D Laplacian: From Cartesian to Spherical Polar Coordinates
Differential forms calculation: the Laplacian in spherical, cylindrical coords (Part 3)
general formula for laplacian || laplacian in spherical || cylindrical || Cartesian system
Easy way to write Gradient and Divergence in Rectangular, Cylindrical & Spherical Coordinate sys...
Gradient, Divergence, Curl And Laplacian in different coordinate systems#gradient #divergence #curl
How to solve differential equations
How REAL Men Integrate Functions
Laplace equation in 45 sec 🤯
Poisson's and Laplace Equations: Derivations and Explanations
Laplace operator question
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Shortcuts/ Vector identities in Vector calculus for Gradient, Divergence, Curl & Laplacian opera...
section 3 3b
EC8451 ELECTROMAGNETIC FIELDS SHORTCUT TO DIVERGENCE FORMULA
Physics Ch 67.1 Advanced E&M: Review Vectors (45 of 55) What is the Laplacian?
deriving gradient divergence laplacian, Curl in cylindrical Coordinates - Part 2
Комментарии
 0:42:33
0:42:33
 0:03:45
0:03:45
 0:28:23
0:28:23
 0:41:01
0:41:01
 0:11:47
0:11:47
 0:05:31
0:05:31
 0:23:21
0:23:21
 0:10:27
0:10:27
 0:20:23
0:20:23
 0:11:16
0:11:16
 0:05:43
0:05:43
 0:16:52
0:16:52
 0:19:37
0:19:37
 0:00:46
0:00:46
 0:00:35
0:00:35
 0:00:49
0:00:49
 0:12:19
0:12:19
 0:01:01
0:01:01
 0:00:16
0:00:16
 0:48:30
0:48:30
 0:21:33
0:21:33
 0:07:50
0:07:50
 0:03:35
0:03:35
 0:16:55
0:16:55