filmov
tv
Physics 8 Work, Energy, and Power (33 of 37) Variable Friction - Example 2
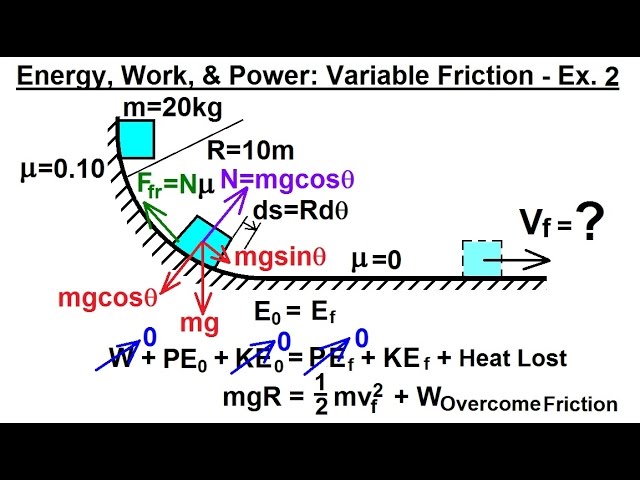
Показать описание
In this video I will find x(final)=? of a 2.0kg block sliding down an arc with a variable coefficient of friction relative to the angle of the arc.
Next video in this series can be seen at:
Work, Energy, and Power: Crash Course Physics #9
Physics 8 Work, Energy, and Power (29 of 37)
A Level Physics Revision: All of Work, Energy and Power (in 18 minutes)
Physics 8 Work, Energy, and Power (22 of 37) Box pushed up a Frictionless incline
Work and Energy
Physics 8 Work, Energy, and Power (23 of 37) Box pushed up a Rough Incline With Friction
Physics 8 Work, Energy, and Power (36 of 37) Dropping an Object on a Spring
Physics 8 Work, Energy, and Power (30 of 37)
Work, Energy and Power - Part 1 | Class 11 Physics | JEE 2025 Preparation | LIVE |@InfinityLearn-JEE
Physics 8 Work, Energy, and Power (26 of 37) A pulley with two weights
Physics 8 Work, Energy, and Power (27 of 37)
Kinetic Energy and Potential Energy
Physics 8 Work, Energy, and Power (31 of 37)
Physics 8 Work, Energy, and Power (25 of 37) Crate slides down a rough incline
Physics 8 Work, Energy, and Power (37 of 37) Pendulum: Example (Cat included)
physics 101 chapter 7 8 Work and Energy part 1
Work and Power in Physics
WORK & ENERGY | Physics Animation
Kinetic Energy and Potential Energy
GCSE Physics - Power and Work Done #7
Work and Energy : Definition of Work in Physics
Physics 8 Work, Energy, and Power (33 of 37) Variable Friction - Example 2
Work, Force & Energy | What Is Force? | Science For Kids | The Dr Binocs Show | Peekaboo Kidz
Physics 8 Work, Energy, and Power (35 of 37) Block Pulled at an Angle
Комментарии
 0:09:55
0:09:55
 0:08:19
0:08:19
 0:18:07
0:18:07
 0:07:49
0:07:49
 0:04:57
0:04:57
 0:10:21
0:10:21
 0:05:19
0:05:19
 0:05:08
0:05:08
 1:09:02
1:09:02
 0:09:54
0:09:54
 0:13:57
0:13:57
 0:04:49
0:04:49
 0:11:08
0:11:08
 0:10:30
0:10:30
 0:04:19
0:04:19
 0:18:02
0:18:02
 0:03:17
0:03:17
 0:04:14
0:04:14
 0:13:18
0:13:18
 0:03:54
0:03:54
 0:11:23
0:11:23
 0:08:45
0:08:45
 0:06:03
0:06:03
 0:08:07
0:08:07