The Fundamental Theorem of Functional Analysis

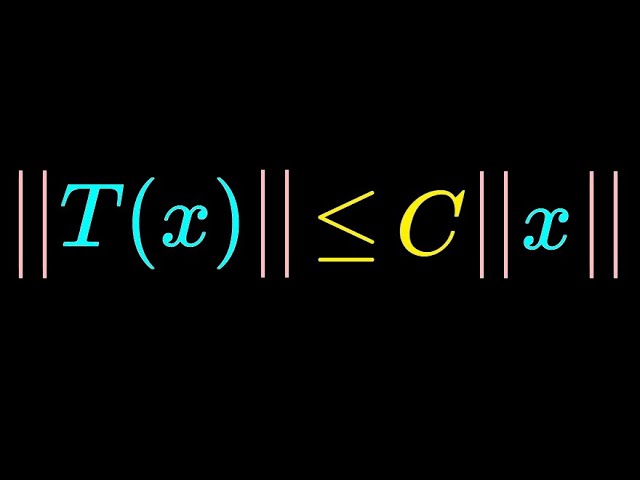
Показать описание

Here is the most important theorem in functional analysis: A linear transformation T is bounded if and only if it is continuous. This allows us to easily check whether an operator is continuous, and is the quintessential fact that is the genesis to the whole field. Enjoy!

Dr Peyam

Рекомендации по теме

Комментарии

I'm watching him for 3 years, I learned a lot, thank you so much 🥰❤❤❤

nourdinespen

More functional analysis and Banach/Hilbert spaces please

riadsouissi

I imagine all the people expecting another video about a fun arithmetic fact, and now it "doesn't even have to be a Banach space" :P. Cool video though!

jenssletteberg

Very nice presentation! As a suggestion for a possible future video, please talk about the Arzela-Ascoli theorem!

LegendOfMurray

YOU ARE AMAZING THANK YOU SO MUCH
You are also very funny by the way XD
You are doing the world a great service just by being yourself and expressing yourself this way!

michaeljagdharry

I've started watching your channel this month. I had heard your name before but never watched a video before than. What I absolutely love about this channel is that your contents are lit and you approach things as a PURE mathematician would (as much as possible on a YouTube video) without using stuff like notation abusing or things that really hit me hard. I'm a physics student, by the way.

CarmeloTLA

Another fantastic video. Thank you Dr. Peyam!

paolasaldarriaga

yay, linear transformations and vector spaces!

bettkitty

Is there an analogy of this for metrics in general?And if so, is the statement " 2 metrics d1 and d2 on V are equivilent iff there is c>0 such that d1(x, y)<=c*d2(x, y) for all x and y in V" the analagous statement? And does equality of them give us a right to use either metric interchangeably in things like limits?

aneeshsrinivas

What would be an example of an unbounded linear transformation? As far as I know T can be represented by a matrix, so couldn't we bound every transformation by some notion of maximum scaling? maybe the max eigenvalue? Hence every linear transformation would be bounded? I've got no notion functional analysis but the title made curious

rob

Can you Explain brich-dyre cojecture and L-function Doctor ?!!

omargaber

Hi, thanks for the video and I have one question: Would it be correct if we didnt set epsilon to be 1 and we chose our constant C to be epsilon/delta?

elhoplita

Isn’t the definition you wrote down for continuity in the beginning real uniform continuity and not general continuity?

Happy_Abe

I would not say Fundamental, but it is used everywhere ^^

selfmade

During the step where you estimate ||T(x delta/||x||)|| you say that ||x*delta/||x|| ||< delta which is obviously wrong as it equals delta. This is precisely why we need the ||v|| < delta => ||T(v)|| < 1 in the first place. Otherwise nice video!

leonardromano

Is oreo healthy now? Not seen it since many videos

adityadwivedi

Hahn--Banach Theorem is definitely more fundamental!

EhsaanHossain

So, only for linear functions including the zero vector?

jkid

Hi DrP, I want you to buy a fairly large canvas (about the size if the board in this vid), and paint it with a coat or two of gesso. Then record an episode on canvas, instead of a board (make it a cool episode). Then sign the canvas, with a small date, and sell it to me.

rexdalit

The definition of "bounded" given here seems to be the definition of Lipschitz continuity?

FT

The Fundamental Theorem of Functional Analysis

The Fundamental Theorem of Functional Analysis

Fundamental Theorem of Calculus Part 1

The Fundamental Theorem of Calculus

Fundamental theorem of calculus (Part 1) | AP Calculus AB | Khan Academy

How REAL Men Integrate Functions

Chapter 3 // Fundamental theorems of // Functional Analysis

The Fundamental Theorem of Calculus

Solving a functional equation that depends on integrals using the fundamental theorem of calculus

Mario Livio: Is God a Mathematician (ch. 9: On the Human Mind, Mathematics and Universe)

MATH 144 - 5.4 - The Fundamental Theorem of Calculus

The Fundamental Theorem of Fourier Series

Real Analysis 56 | Proof of the Fundamental Theorem of Calculus

Fundamental Theorem of Calculus, Accumulation Functions - Calculus

The Fundamental Theorem of Calculus Introduction

Math 441 - 7.5 Fundamental Theorem of Calculus

Real Analysis 54 | First Fundamental Theorem of Calculus

Real Analysis 55 | Second Fundamental Theorem of Calculus

28.1 The fundamental theorem of calculus

Using the First Fundamental Theorem of Calculus

Fundamental Theorem of Calculus, Accumulation Functions - Calculus

Using the Fundamental Theorem of Calculus

Introduction to Density Functional Theory [Part One] Background

The First Fundamental Theorem of Calculus, Final Problem 4

The Fundamental Theorem for Gradients with Example | Vector Calculus | Lecture 8