Magnetic Field from a Circular loop

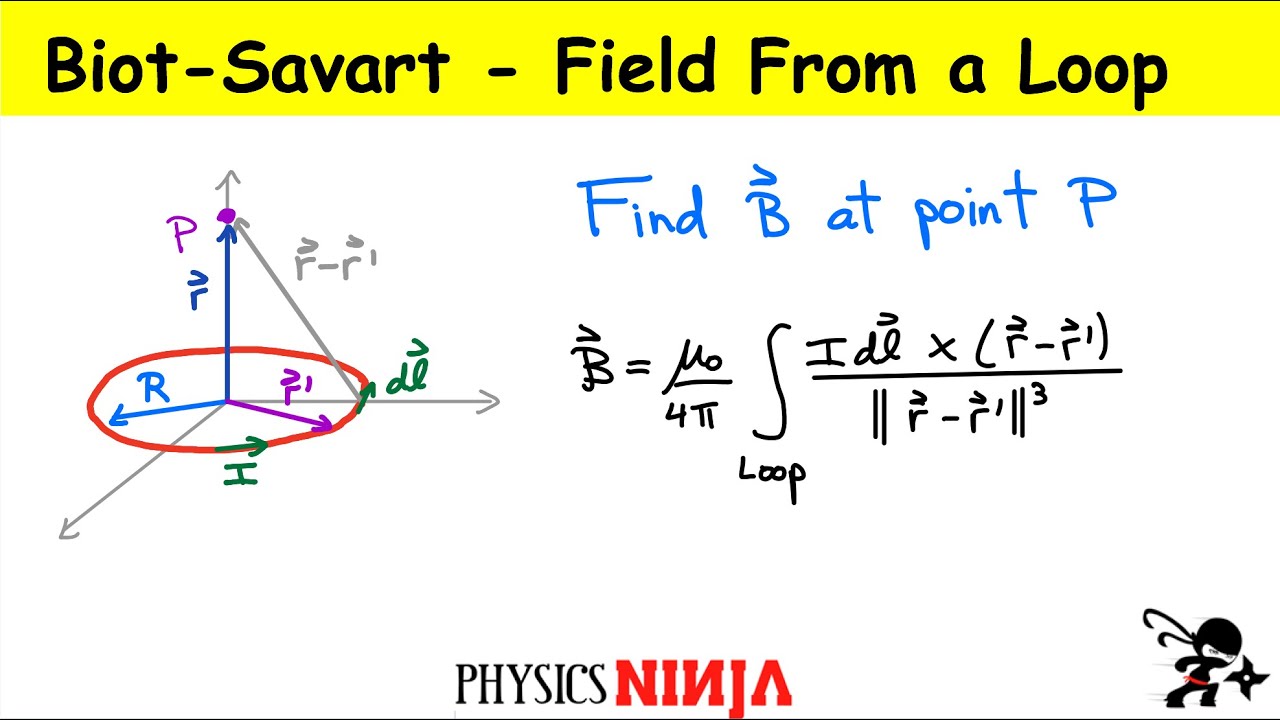
Physics Ninja looks at the magnetic field produced by a circular loop.

The Biot Savart law is used to find the total field produced by the loop at a point above the plane of the loop.

[illiztDesignsHD]

This video is excellent, please don't stop making tutorials! Maybe some Lagrangian and Hamiltonian mechanics also?

[Hero-zqdh]

What happens to the angle that come from the cross product in the beginning?

[seniorshimhanda]

Excellent video as usual. How about a video on the magnetic fields for spiral square and circular coils?
Comparison between the two is a hot topic in wireless power transfer.

[stevenshum]

Love this question. I have to constantly refer to this example to learn Biot-Savart law.

[baukenieuwenhuis]

only thing I have to say is that the cross product can be defined better. It has to be perpendicular to both vectors but there are two solutions to this, and you did not specify why you took the vector pointing up right instead of down left, which would also fit the parameters

[MonseMania]

Thank you ! Have a final in T-11 hours and this helped explain the law and mathematics of it well.

[fsilveyra]

This is the best explanation out there, thank you!

[vikramnagarjuna]

Hi this is vikram from India,
Please post more videos as this is lock down time due to Corona virus.
I love your videos.

[dalenassar]

What about B at a point offset from the center?
Great Videos...

[hanazaimovic]

hi, I know it's been two years since you posted the video but I hope you can help me. You explain perfectly and I understood everything, except why at the very beginning the formula says that the magnetic field is inversely proportional to 4π instead of 2π

[minhokim]

Nice video, Thanks. Could you make another at points of off axis?

[danielstocks]

Hi,
This video was very useful. Would you be able to do a video of the same principle but if the point P is not on the central axis. So still in the same parallel plane of the loop but displace by an angle?
That would be incredible

[joaoafonso]

im sorry but isnt the magnitude missing the sin of the angle between dl and r - r' ?

[euanwilliams]

Great video; the only thing I don’t quite understand is why theta for dBz is the same as for the triangle with r-r1, z and R. Would you mind explaining that, please?

[enejedhddhd]

I understand the math however, id like to ask if you integrated upon dB without multiplying by costheta.

[trismegistus]

09:25 I think the Z component is should be dB.cos(theta), not sinuse.

[paulguillermo]

Find the exact magnetic field along the z-axis of a hexagonal loop with side a, which carries a steady current I. Find the approximate magnetic field at large distances from the loop by computing the dominant term in the multipole expansion of the magnetic vector potential of the loop. Show that for large values of z along the axis the two approaches give the same result.

[gosnfrenki]

I cant understand why is sin and no cos theta?? I put theta where you put it... the oposite angle from theta is theta again on the other side... Method of apex angles gives me that theta is upper angle on the right side... Wish I understand this...