filmov
tv
Differential Geometry: Lecture 5 part 1: frames and components in R3
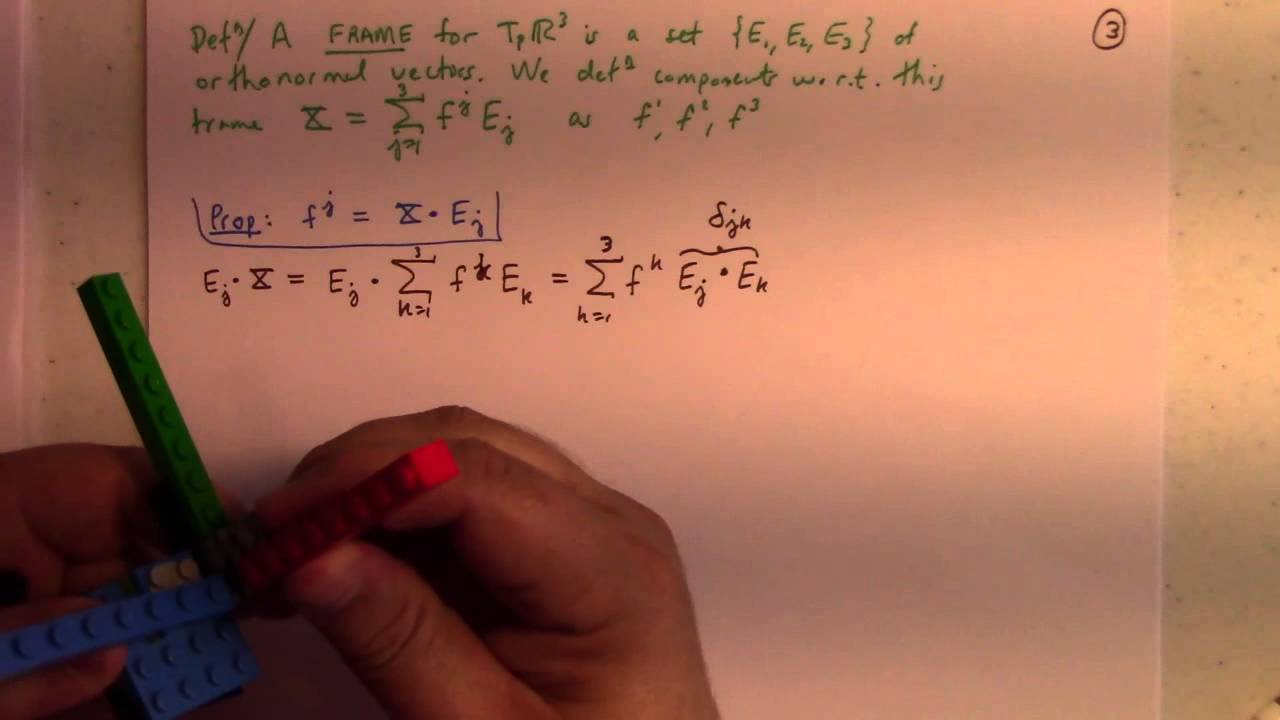
Показать описание
Here we briefly discuss how R3 is a metric space, an inner product space and a normed linear space as the relate to the usual dot product. Then we explain how the dot and cross products are constructed on the tangent space at p. Orthonormal sets are defined. We see how dot products allow us to select components with respect to an orthonormal basis. The term frame is introduced and we see how the cross and dot product formulas naturally transfer to components of a vector field w.r.t. a frame. Finally, 4 example frames are given. Next part we begin with the Attitude matrix etc.
 0:53:32
0:53:32
 0:46:28
0:46:28
 0:57:11
0:57:11
 0:45:20
0:45:20
 1:27:49
1:27:49
 0:44:51
0:44:51
 1:19:25
1:19:25
 0:51:21
0:51:21
 1:00:26
1:00:26
 0:37:40
0:37:40
 0:49:12
0:49:12
 0:09:40
0:09:40
 0:13:57
0:13:57
 0:36:29
0:36:29
 0:50:47
0:50:47
 0:11:16
0:11:16
 0:12:31
0:12:31
 0:00:35
0:00:35
 0:00:37
0:00:37
 0:01:00
0:01:00
 0:00:19
0:00:19
 0:00:11
0:00:11
 0:49:32
0:49:32
 0:53:32
0:53:32