filmov
tv
Python Tutorial deutsch, Das 100 Gefangene Problem

Показать описание
Hier simulieren wir unterschiedliche Strategien beim 100 Gefangenen Problem.
Python Tutorial deutsch, Das 100 Gefangene Problem
Python Tutorial Deutsch: Lerne Python in einer Stunde
Python Tutorial für Anfänger꞉ Lerne Python in 60 Minuten (deutsch)
PYTHON LERNEN in 10 Minuten (Anfänger Tutorial Deutsch)
Python Tutorial Deutsch (Komplettkurs) - Python lernen in unter 4 Stunden
PYTHON TUTORIAL AUF DEUTSCH - In einer Stunde Python lernen!
Python Tutorial Deutsch | Komplettkurs für Anfänger
Python Tutorial für Data Science | Komplettkurs Deutsch
🎬 Video mit PYTHON schneiden (unter 100 Zeilen Code)!
Python Tutorial | Array 💡 und Liste | (Deutsch)
Python lernen | Kompletter Anfängerkurs
New Python Coders Be Like...
Python Tutorial deutsch [5/24] - Datentypen (int, float und str)
Python Tutorial deutsch, Geschachtelte Schleifen vermeiden
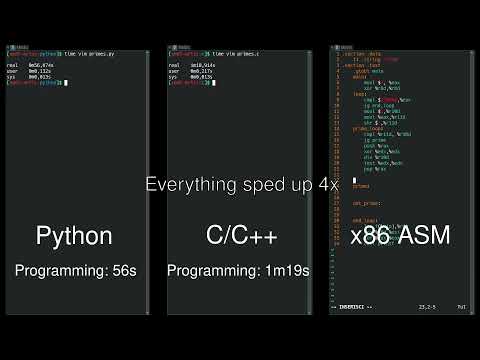
Python vs C/C++ vs Assembly side-by-side comparison
Python Full Course for free 🐍
Python Tutorial deutsch, Fraktaler Baum
Programmiere deine erste KI mit Python | 30min Tutorial
Deep Learning Cars
ALLE Python Keywords in EINEM Video erklärt | #Python
Python Tutorial - Python Full Course for Beginners
Python Tutorial deutsch, Rechnen mit Zeiten
Python auf dem Raspberry starten
Python Tutorial deutsch [4/24] - Variablen
Комментарии
 0:23:56
0:23:56
 1:09:12
1:09:12
 1:11:57
1:11:57
 0:12:40
0:12:40
 3:22:17
3:22:17
 1:10:07
1:10:07
 6:15:55
6:15:55
 0:54:41
0:54:41
 0:04:49
0:04:49
 0:06:41
0:06:41
 3:58:09
3:58:09
 0:02:13
0:02:13
 0:10:27
0:10:27
 0:13:39
0:13:39
 0:01:01
0:01:01
 12:00:00
12:00:00
 0:28:07
0:28:07
 0:29:07
0:29:07
 0:03:19
0:03:19
 0:14:06
0:14:06
 6:14:07
6:14:07
 0:25:58
0:25:58
 0:04:02
0:04:02
 0:10:50
0:10:50