Crack the Code of Complex Powers: Finding the Principal Value of (1+i)^(4i)

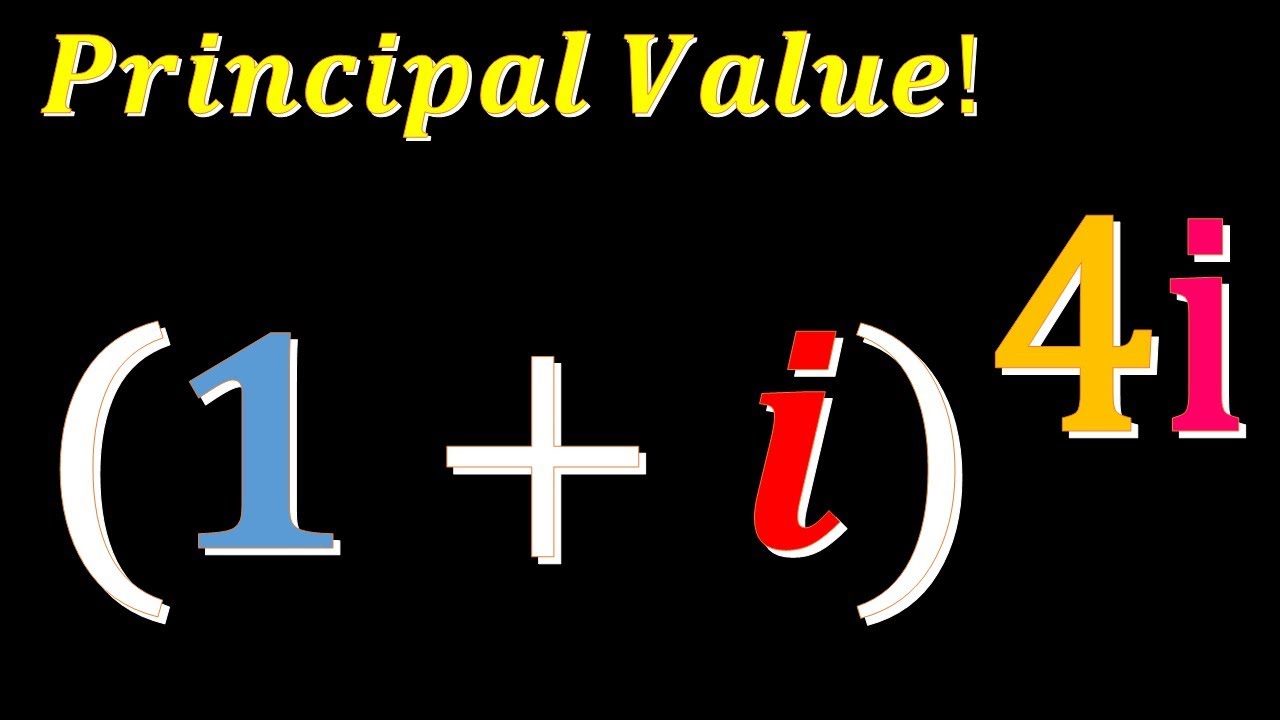
preview_player
Показать описание
Dive into the world of complex numbers and unlock the secret to calculating complex powers like (1+i)^(4i). This video breaks down the process step-by-step, using clear explanations and helpful visuals. Perfect for students, math enthusiasts, or anyone curious about complex numbers!
  1. The Mathmagic Show
  2. complex numbers
  3. complex analysis
  4. imaginary numbers
  5. exponential form
  6. Euler's formula
Рекомендации по теме
Crack the Code 0:02:11

Crack the Code (Black Mous) GUIDE | DMZ Season 4 Mission Guide | Vondel Guide

Crack The Code 0:07:39

Crack The Code Mission Guide For Season 4 Warzone DMZ (DMZ Tips & Tricks)

Crack The Code 0:04:37

Crack The Code DMZ Black Mous Quick Guide Koschei Complex

Crack the Code: 0:01:00

Crack the Code: Conquer this Complex Math Puzzle

How to complete 0:07:28

How to complete 'Crack The Code' DMZ Black Mous Tier 5 'Story Mission'

Crack the Code 0:05:49

Crack the Code of Complex Powers: Finding the Principal Value of (1+i)^(4i)

Cracking the Uncrackable 0:06:22

Cracking the Uncrackable Code 😏

DMZ Crack the 0:01:20

DMZ Crack the Code Mission Guide

The End is 5:00:00

The End is near

Mastering Square Root 0:02:23

Mastering Square Root Exponent Math: Crack the Code of Complex Problems!

Crack the Code 0:45:39

Crack the Code of Complex Deals: The Hidden Truths REVEALED with Lawrence Lanzilli

Worlds First Solo 0:04:37

Worlds First Solo Diamond Safe | Crack The Code

DMZ Crack The 0:11:18

DMZ Crack The Code Mission Guide (SOLO) Season 5 - How to Unlock Weather Proof Operator Skin

Crack the Code 0:00:32

Crack the Code of This Complex Riddle! 🕵️‍♂️🔢

Crack the Code 0:02:21

Crack the Code to Solve this Puzzle | What is the Password

DMV Permit Test 0:00:15

DMV Permit Test App - Crack the Code of Complex Intersections

Crack the Code 0:00:53

Crack the Code of Circuits! Quick and Exciting Breakdown.

🔐 Crack the 0:00:21

🔐 Crack the Code: 10 Complex Riddles to Challenge Your Puzzle-Solving Skills! 🧠'

Crack the Code: 0:00:50

Crack the Code: Solving a Complex King Pawn Endgame Puzzle! - Day 33

The Science of 0:08:21

The Science of Codes: An Intro to Cryptography

Crack the Code: 0:00:31

Crack the Code: Can You Solve This Complex Riddle Challenge? 🤔🔢

[English] Crack the 0:02:03

[English] Crack the code to solve complex 3 digit Multiplication problems

Crack the Code: 0:00:31

Crack the Code: Can You Solve This Complex Riddle?

Crack the Code 0:00:20

Crack the Code to Healthcare Success! 💼🔍

Комментарии
Автор

ln(2^2.5) after simplification in the last step

tomsmith
Автор

(1+i)^(4i) = ((1+i)^4)^i = (-4)^i = (i^2i)4^i = e^(-π).4^i = e^(-π).(cos ln(4) + i.sin ln(4)). A slightly cleaner form of your end result.

Now a puzzle…. What is i^(4i)?

Is it = (i^i)^4 = [e^(-π/2)]⁴^4 = 0.2078… ^4 = 0.016… ?

OR

(i^4)^i = 1^i = 1 ?

OR is it both?

Note: x^i = e^(i.lnx) = cos(lnx) + i. sin(lnx). Thus 1^i = 1

ianrobinson
Автор

Please solve (1+i)^(2-i)
Principal value and general value

mr.unique
Автор

how would u use the principal to go backwards?

LP-htir