Quantum Spectrum in Algebraic Geometry I

Speaker: Maxim Kontsevich
Affiliation: IHES and University of Miami
01/27/20

The name ‘Quantum Spectrum’ in the title refers (for a compact symplectic manifold) to the spectrum of the operator of quantum multiplication by the first Chern class of the tangent bundle, considered as a multi-valued function on the Frobenius manifold encoding genus=0 Gromov-Witten invariants.

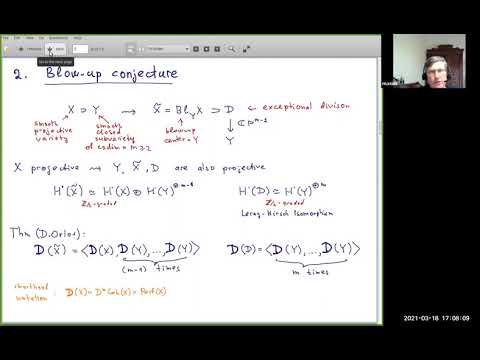
In the algebraic case, for complex projective varieties, one of the greatest not yet understood mysteries known from early days of mirror symmetry, is a conjectural relation (by S.Barannikov, B.Dubrovin and myself) between the quantum spectrum and semi-orthogonal decompositions of the derived category of coherent sheaves. We are very far from even approaching this problem in complete generality, beyond particular explicit examples.

The main goal of the lectures is the formulation of quantum blow-up formula which seems to be totally within reach, leading to numerous consequences in the mainstream algebraic geometry.

One application is the construction of a new very strong birational invariant (also for non-algebraically closed base fields). In particular, one can deduce non-rationality of a generic cubic 4-fold over complex numbers. Another application is a construction of a new exotic motivic measure. More speculatively, one can have a relation to Minimal Program, a categorification of intersection cohomology for varieties with canonical singularities, and an obstruction to the strong resolution of singularities in positive characteristic.