filmov
tv
Gaussian Quadrature 2: How to Determine the Weights

Показать описание
Gaussian Quadrature 2: How to Determine the Weights
Gaussian Quadrature | Lecture 40 | Numerical Methods for Engineers
Chapter 07.05: Lesson: Two Point Gauss Quadrature Rule: Example
Numerical Analysis: Gaussian Quadrature
Numerical Integration - Gauss Quadrature 2 Point Formula
Quick Revision of Gauss Quadrature Formula| Direct Example| One point|Two Point| Three Point Formula
Gaussian Quadrature
An introduction to numerical integration through Gaussian quadrature
Gauss Quadrature 2-Point Method (Numerical Integration) on Casio fx-991ES Scientific Calculator
Gauss-Legendre Quadrature 2: Solving the equations
The Short Derivation of the Two-Point Gaussian Quadrature Rule. Full Derivation Link in Description
Problems on Gauss-Quadrature 2-point and 3-point formula by Keshav Jadhav
Gaussian Quadrature - Exercise 2: Single variable function over an arbitrary interval
ch4 C: Gaussian quadrature, part 2. Wen Shen
Advantage of using Gaussian quadrature
Gaussian Quadrature - Analysis
Preview: The Magic of Gaussian Quadrature - A Billion Times Better than the Next Best Thing
Unlock Precision: Mastering Gauss Quadrature 2-Point Formula | Advanced Numerical Integration
Numerical Integration - Gaussian Quadrature
A brief introduction to Gauss quadrature
Gaussian quadrature 2-point & 3-point formula | Problem in Tamil
Gaussian quadrature
Gauss Quadrature formula
Gaussian Quadrature 1: Summary of Legendre Polynomials
Комментарии
 0:12:34
0:12:34
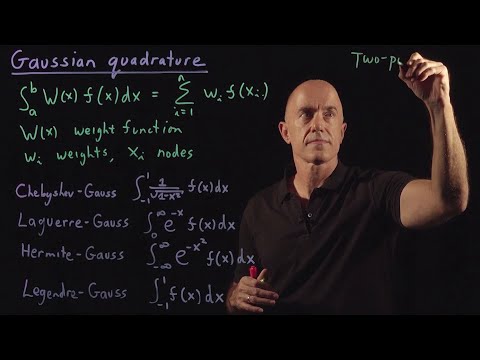 0:08:51
0:08:51
 0:07:35
0:07:35
 0:36:20
0:36:20
 0:06:50
0:06:50
 0:04:05
0:04:05
 0:20:49
0:20:49
 0:26:04
0:26:04
 0:06:00
0:06:00
 0:15:14
0:15:14
 0:12:50
0:12:50
 0:10:16
0:10:16
 0:12:10
0:12:10
 0:08:25
0:08:25
 0:06:36
0:06:36
 0:18:41
0:18:41
 0:09:35
0:09:35
 0:00:58
0:00:58
 0:17:17
0:17:17
 0:11:13
0:11:13
 0:12:56
0:12:56
 0:18:54
0:18:54
 0:00:16
0:00:16
 0:09:19
0:09:19