Limit of absolute value functions [ lim |x^3 - x|/(x^3 - |x|) as x goes to 0 ]

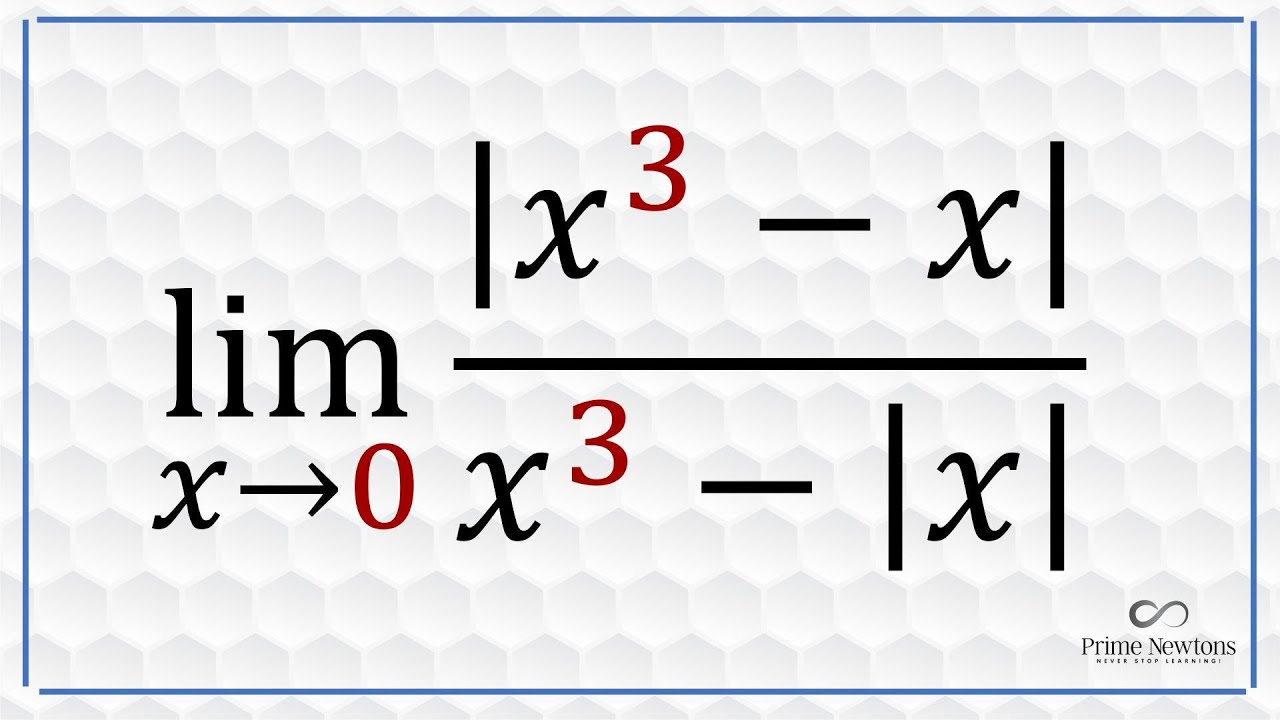
Показать описание

In this video , I showed how to compute the limit of all absolute value functions

Рекомендации по теме

Комментарии

fr the most underrated education youtuber

JaydenPatrick-jymr

Newtons, your explain is really excelent....

vitotozzi

We can do this without worrying about approaching from left or right actually. The key is realizing x^3 = x* x^2 = x*|x||x|.

f(x) = |x^3 - x| / (x^3 - |x|)
= (|x|*|x^2 - 1|) / (x*|x||x| - |x|)
= |x^2 - 1| / (x|x| - 1)

Taking the limit to 0 gives us |-1| / (-1) = 1/(-1) = -1

aavalos

amazing explanation, thank you so much.

sanam

I would've gotten this wrong, at least on the first pass. I wouldn't have considered that the range from -1 to +1 behaves differently.

kingbeauregard

I found an easier way. First divide both numerator and denominator by |x|. Then the numerator becomes |x^2-1|. The denominator becomes

x^3/|x|-1

which simplifies to x|x|-1. Thus we have the limit of

|x^2-1|/(x|x|-1).

Plug in 0 and we get |-1|/(-1)=-1.

GreenMeansGOF

I expanded the fraction by modulo x and diveded numeretor and denominator and subtituted x equal to zero.

Gleb

This function has such a cool-looking graph.

mattbrown

9:52 but if you're looking for x > 0 then not only 0<x<1 applies, but x>1 also (which changes the sign of the limit). What am I missing?

rimantasri

Two conditions: x is positive or negative!

張茗茗-yi

Use |x^3-x| = |x.(x^2-1)| =|x|.|x^2-1| and in the denominator x^3-|x| = |x| .( |x|.x-1), it will be more simpler to prove.

pratapray

Beauty limits are even: a) V(x-1)/(Vx-1) when x goes to 1 b) (8^x-1)/(4^x-1) when x goes to 0 c) (4^x-2^x)/(2^x-1) when x goes to 0 d) [log with base 2 of (x-1)]/[(log with base 2 of x)-1] when x goes to 2. 😀😉

klementhajrullaj

And if, |x^3-x|/(|x^3|-|x|), or |x^3-x|/(|x^3|-x)??? ...

klementhajrullaj

Autre solution.
Au voisinage de 0, un polynôme est équivalent à son terme non nul de plus bas degré.
Si x>0, au voisinage de 0, x³ - |x| = x³ - x ~ -x = -|x|
Si x<0, au voisinage de 0, x³ - |x| = x³ + x ~ x = -|x|
|x³ - x|/(x³ - |x|) ~ |x³ - x|/(-|x|) = - |x² - 1| (Indépendamment du signe de x)
Ce qui tend vers -1 si x tend vers 0.

michelmegabacus

No need of simplifying so much,
Left hand Limit = -1
Right Hand limit = -1

Hence limit is -1

samar

Limit of absolute value functions [ lim |x^3 - x|/(x^3 - |x|) as x goes to 0 ]

Limits and Absolute Value

Limit of Absolute Value Function

Limit of Absolute Value Function (II)

Limit of absolute value functions [ lim |x^3 - x|/(x^3 - |x|) as x goes to 0 ]

Learn to evaluate the limit of the absolute value function

Limits of Absolute Value Functions

Algebraic Limits: Absolute Value

Limit of Function with Absolute Values Involved TIPS

Prove using epsilon-delta: Limit of (2x^2 - 3x + 1)/(x^3 + 4) = 1/4 as x approaches 2

Limit of Absolute value Functions

Limits Involving Absolute Value (AP Calc)

Find the One-Sided Limit with Absolute Value: |x|/x as x approaches zero from the Left #shorts

Limits involving Absolute Value | Limits and Absolute Value | Calculus

How to Compute a One Sided Limit with an Absolute Value

Calculus I: Limit with Absolute Value (Hard Example)

Finding One-Sided Limits of Piecewise and Absolute Value Functions | Calculus

Finding Limits of Functions with Absolute Value | Calculus 1 | Math with Professor V

Limit of Expression with Absolute Function and Graph

Limits in Absolute Value Functions - (Limits - 3)

Finding Limits of Functions with Absolute Value | Calculus 1 | Math with Professor V

Limits Involving Absolute Value Functions Calculus 1 AB

Absolute Value Limit: x/|x| as x approaches zero from the left #shorts

Determine Limit Involving Absolute Function

Limits with Absolute Value Functions