Interval Scheduling ( Greedy Algorithm ) - Algorithms

Thanks for subscribing!

---

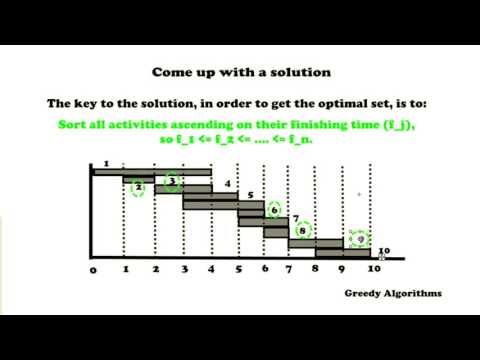
This video is about a greedy algorithm for interval scheduling.
The problem is also known as the activity selection problem.
In the video the following concepts are explained:
- The problem
- The solution to the problem
- The pseudocode for the solution
- The running time of the provided pseudocode.
- A proof that shows that the solution is right
- Some tips on the implementation

---

If you thought this video was useful, make sure to give it a like!
If you want to support this channel, make sure to subscribe.
If you have any questions, use the comment section.

This video has been published by MisterCode.

[savannahpleau]

Thank you so much! You help me so much in school!

[affyne]

"so too bad for a pretty girl, we're not going to date her today." ikr, programmers never date

[SuperSlugger]

I thought the proof should prove that the algorithm solves the scheduling problem and also prove that the solution is always optimal (always finds the maximum number of disjoint/non-overlapping tasks).

[vincit]

Great Video! Now I unterstand the algorithm.

[amandachan]

From an implementation perspective, if you use a set there is no guarentee that you can check the most recent end time against your current start time in O(1) time because sets are unordered. I think using an array and checking the last element in the array against your jth element would give you the desired O(n) in the for loop. But thank you for the explanation, great vid! <3

[FilipLindahl]

Great video! It really helped clarify the algorithm.

[潘潘舆]

what is the cost of checking activity j is compatible with A? I think it should be 1+2+...+n = O(n^2). A little bit confused about that.

[SaiKrishna]

I guess we need to prove the elements in result are compatible and the number of elements in the set is maximum(optimal). you proved elements compatibility but u missed the maximum result set part.

[arunkanakarajan]

Instead of sorting the jobs in the ascending order of earliest finish time,
can we choose to sort the jobs in the descending order of farthest start time? Is it optimal.. Can you explain for this case?

[ylamummo]

What about the following problem: We are given n activities (each with starting and ending times) and also q plans (also with starting and ending times). Now we want to determine for every plan the maximal amount of activities we can do during that time interval. How could we solve this problem efficiently? That is, without having to iterate through all the activties in the plan intervals over and over again which would lead to a time complexity of O(nq + nlogn) (nlogn for sorting in the beginning and then n time for every plan). What could we do to make this term nq smaller?

[NitishRaj]

If each activity associated with Profit(>=0) Can you apply greedy to maximize Profit instead of maximizing no of activities ?

[skinpa]

Don't you have to prove that A is optimal, not that everything in A is compatible?

Also, isn't this proof a bit circular? Your goal is to show that if you add j to A, everything is still compatible. But the reason for it is because if you add j to A, it must mean that everything is compatible.

[akshaybhatt]

Is this prove for checking feasiblity of interval scheduling?

[cm]

+MisterCode so this algorithm produces always an optimal solution?

[sahayayush]

whats the difference between activity selection problem nd interval scheduling problem?

[__kpsingh__]

I would have made 8-10 compatible at all costs.

[parsanoori]

You didn't prove that the algorithm maximizes the the amount of activities.