filmov
tv
finding ALL pythagorean triples (solutions to a^2+b^2=c^2)

Показать описание
For more calculus tutorials, check out my new channel @bprpcalculusbasics
finding ALL pythagorean triples (solutions to a^2+b^2=c^2)
2023 Number Challenge: Find all Pythagorean triples that contain number 2023
Finding all Pythagorean Triples
Pythagorean Triples
All possible pythagorean triples, visualized
Euclid - How to find all possible Pythagorean Triplets?
Finding Pythagorean Triples Using Simple Geometry
Finding all the Smallest Pythagorean Triples (Livestream)
Number Theory | Primitive Pythagorean Triples
Finding Primitive Pythagorean Triples - using formula
Japanese Method #shorts #fyp
Pythagorean Triples - CodeForces Educational Round 104 Problem D solution WITH CODE| Algorythm
Finding Pythagorean Triples using Algreraic Methods
Pythagorean Triplet - Coding Interview Question
Finding Pythagorean Triplets | Class 8 | Learn With BYJU'S
Parametrizing all Pythagorean Triples
Formula for Generating ALL Pythagorean Triples
Pythagorean Triples and it's Applications | Week 1 | GSHOC
Direct Parametrization of Pythagorean Triples
Pythagorean Triples (and Quadruples) Are Everywhere!
Method to Generate Pythagorean Triples and Verify Formula
India vs japan || mathematics challenge || 😅🤣🤣🤭
Vedic Maths Trick🔥 | Vedic Maths vs Normal Maths #fun #shorts #youtubeshorts #trending #vedicmaths...
C program to find all Pythagorean triplets in a given range of numbers
Комментарии
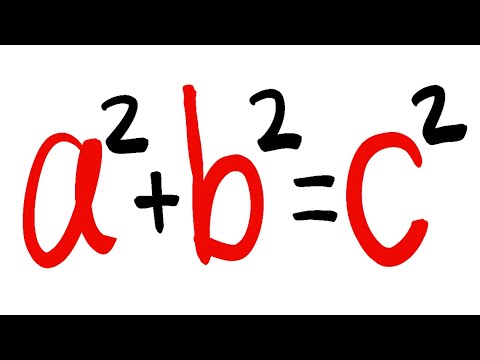 0:12:18
0:12:18
 0:08:22
0:08:22
 0:15:41
0:15:41
 0:08:59
0:08:59
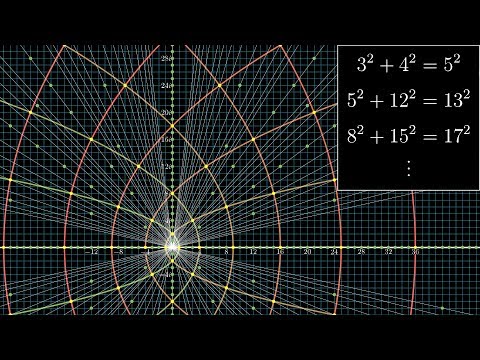 0:16:58
0:16:58
 0:19:32
0:19:32
 0:03:14
0:03:14
 1:48:43
1:48:43
 0:19:50
0:19:50
 0:09:06
0:09:06
 0:00:20
0:00:20
 0:16:26
0:16:26
 0:11:44
0:11:44
 0:10:47
0:10:47
 0:05:26
0:05:26
 0:08:33
0:08:33
 0:30:21
0:30:21
 1:16:55
1:16:55
 0:13:42
0:13:42
 0:21:29
0:21:29
 0:16:07
0:16:07
 0:00:12
0:00:12
 0:00:11
0:00:11
 0:05:59
0:05:59