filmov
tv
Can You Solve this Geometry Puzzle?

Показать описание
There are 5 semicircles and the three below have a diameter of 4. Can you find the total red area?
This geometry puzzle was asked by Twitter user @Cshearer41. Please give her a follow if you enjoy geometry puzzles.
Subscribe!
This geometry puzzle was asked by Twitter user @Cshearer41. Please give her a follow if you enjoy geometry puzzles.
Subscribe!
Can you solve this Geometry Puzzle?
Can you solve these geometry problems?
Geometry Problem | Finding the Missing Angle | SAT Prep | Math Problem
Geometry everyone should learn
How To Solve The Hardest Easy Geometry Problem
Missing Angles Geometry Problem | Tricky Math Question | JusticeTheTutor #maths #math #shorts
Can you find the red area? – Geometry puzzle
Solving a geometry question that no one can figure out
Geometry: Can You Solve for x Using Angle Rules? - SAT Math
Geometry | Find the angle #math #tutor #mathtrick #learning #geometry #angles #x
Can you solve this interesting geometry challenge?
■ Can you solve this Geometry question? | Out the box thinking 🧠 Geometry Q2 📐
Incredible trick to solve this geometry problem
Can You Find Angle X? | Geometry Challenge!
Can You Solve This Grade 12 Geometry Problem From Australia? The Marshmallow Chocolate Puzzle
Geometry you need to know for college
VERY HARD South Korean Geometry Problem (CSAT Exam)
Clever method to solve a tricky geometry problem!
Find Missing Side Length Using SohCahToa Trig in Geometry
Can you find the diagonal length X? | (Semicircle) | #math #maths | #geometry
If you can solve this 3d geometry problem, you are a genius
Can you solve these viral geometry problems?
Want to PASS Geometry? You better know this…
That's How You Solve a Geometry Problem!
Комментарии
 0:06:09
0:06:09
 0:09:46
0:09:46
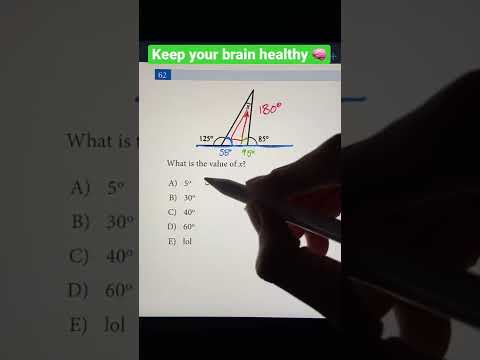 0:00:44
0:00:44
 0:00:15
0:00:15
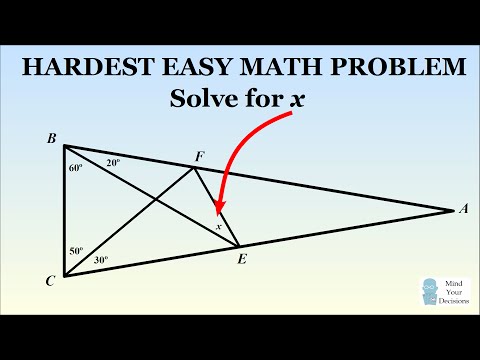 0:08:05
0:08:05
 0:00:37
0:00:37
 0:06:27
0:06:27
 0:03:42
0:03:42
 0:04:19
0:04:19
 0:00:16
0:00:16
 0:10:12
0:10:12
 0:09:43
0:09:43
 0:05:39
0:05:39
 0:08:44
0:08:44
 0:04:13
0:04:13
 0:00:55
0:00:55
 0:12:13
0:12:13
 0:03:15
0:03:15
 0:00:48
0:00:48
 0:09:06
0:09:06
 0:05:58
0:05:58
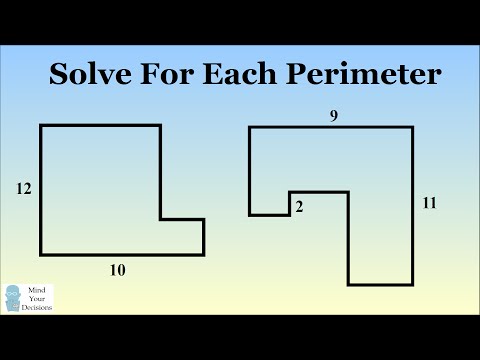 0:04:12
0:04:12
 0:14:08
0:14:08
 0:00:54
0:00:54