filmov
tv
Cracking the Challenge of a Reciprocal Equation
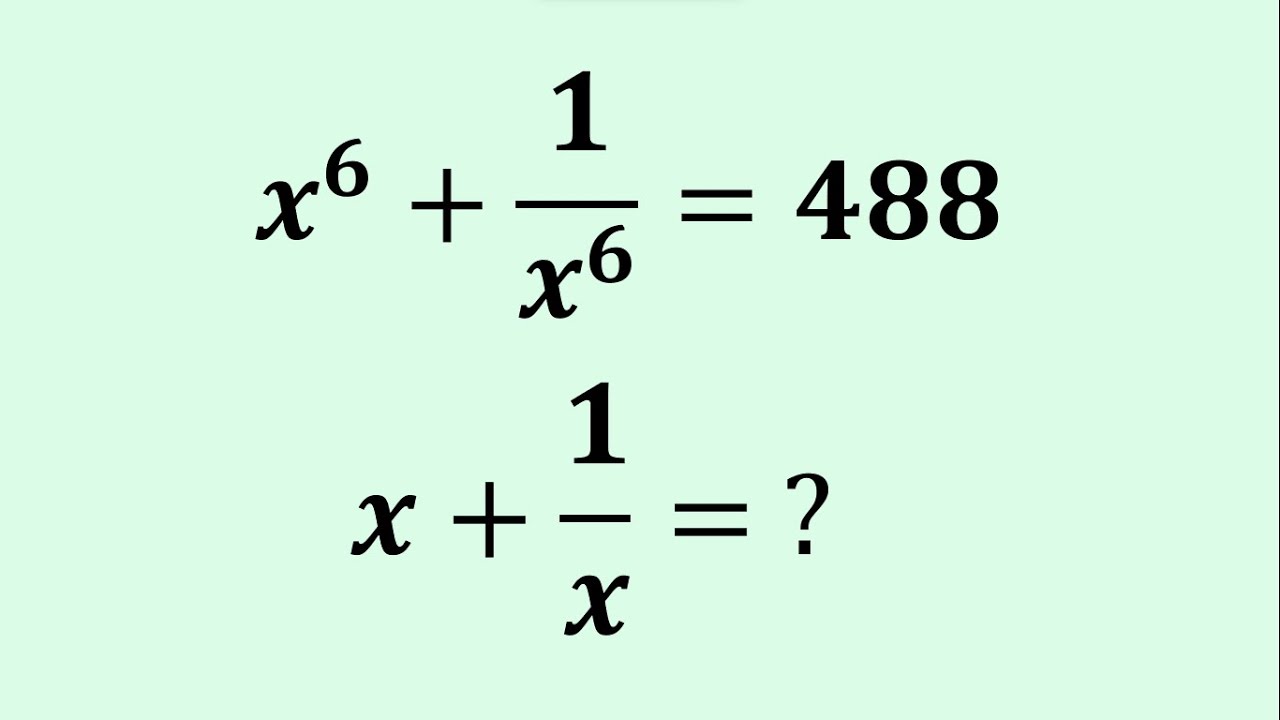
Показать описание
Cracking the Challenge of a Reciprocal Equation
🔍 Ready to crack the code? Join us in "Cracking the Challenge of a Reciprocal Equation" and unlock the secrets of algebraic mastery! 🧠🔢 In this immersive tutorial, we dive deep into the complexities of reciprocal equations, providing step-by-step solutions and insights. Whether you're a math enthusiast or gearing up for an algebraic challenge, this video is your key to conquering the uncrackable. Let's break through together! 🚀🎓 #ReciprocalEquation #AlgebraChallenge #ProblemSolving #CrackTheCode #MathMastery #EquationSolutions #LearnMath #AlgebraicThinking #Mathematics #EducationalVideo #SolveLikeAPro #MathEnthusiast #ChallengeAccepted #AlgebraicProwess #MathJourney #CrackTheChallenge
Topics covered:
Algebra Challenge
Reciprocal equation
How to simplify Expressions?
Math Olympiad
Algebra
Math Tricks
Algebraic identities
Algebraic manipulations
Substitutions
Real Solutions
Exponents
Quadratic equations
Algebraic Challenging Equations and Expressions
Expression
Math Olympiad Preparation
Time-stamps:
0:00 Introduction
0:52 Algebraic identities
1:58 Substitution
4:00 Algebraic manipulations
6:02 Quadratic equation
7:26 Solutions
8:33 Evaluating Expression
Don't forget to subscribe and hit that notification bell to stay updated and smash that like button!
We'd love to hear from you! Did you manage to solve the equation? What other math problems would you like us to cover? Let us know in the comments below!
🎓 Happy learning, and see you in the next video! 🎉
Thanks for Watching !!
@infyGyan
🔍 Ready to crack the code? Join us in "Cracking the Challenge of a Reciprocal Equation" and unlock the secrets of algebraic mastery! 🧠🔢 In this immersive tutorial, we dive deep into the complexities of reciprocal equations, providing step-by-step solutions and insights. Whether you're a math enthusiast or gearing up for an algebraic challenge, this video is your key to conquering the uncrackable. Let's break through together! 🚀🎓 #ReciprocalEquation #AlgebraChallenge #ProblemSolving #CrackTheCode #MathMastery #EquationSolutions #LearnMath #AlgebraicThinking #Mathematics #EducationalVideo #SolveLikeAPro #MathEnthusiast #ChallengeAccepted #AlgebraicProwess #MathJourney #CrackTheChallenge
Topics covered:
Algebra Challenge
Reciprocal equation
How to simplify Expressions?
Math Olympiad
Algebra
Math Tricks
Algebraic identities
Algebraic manipulations
Substitutions
Real Solutions
Exponents
Quadratic equations
Algebraic Challenging Equations and Expressions
Expression
Math Olympiad Preparation
Time-stamps:
0:00 Introduction
0:52 Algebraic identities
1:58 Substitution
4:00 Algebraic manipulations
6:02 Quadratic equation
7:26 Solutions
8:33 Evaluating Expression
Don't forget to subscribe and hit that notification bell to stay updated and smash that like button!
We'd love to hear from you! Did you manage to solve the equation? What other math problems would you like us to cover? Let us know in the comments below!
🎓 Happy learning, and see you in the next video! 🎉
Thanks for Watching !!
@infyGyan
Комментарии
 0:00:22
0:00:22
 0:00:24
0:00:24
 0:03:14
0:03:14
 0:00:18
0:00:18
 0:00:15
0:00:15
 0:01:04
0:01:04
 0:22:16
0:22:16
 0:02:56
0:02:56
 0:00:20
0:00:20
 0:03:14
0:03:14
 0:03:49
0:03:49
 0:00:25
0:00:25
 0:00:23
0:00:23
 0:09:36
0:09:36
 0:00:13
0:00:13
 0:00:15
0:00:15
 0:00:32
0:00:32
 0:00:58
0:00:58
 0:00:36
0:00:36
 0:00:14
0:00:14
 0:00:23
0:00:23
 0:00:30
0:00:30
 0:00:16
0:00:16
 0:02:18
0:02:18