filmov
tv
be careful when an imaginary number is raised to a fractional power
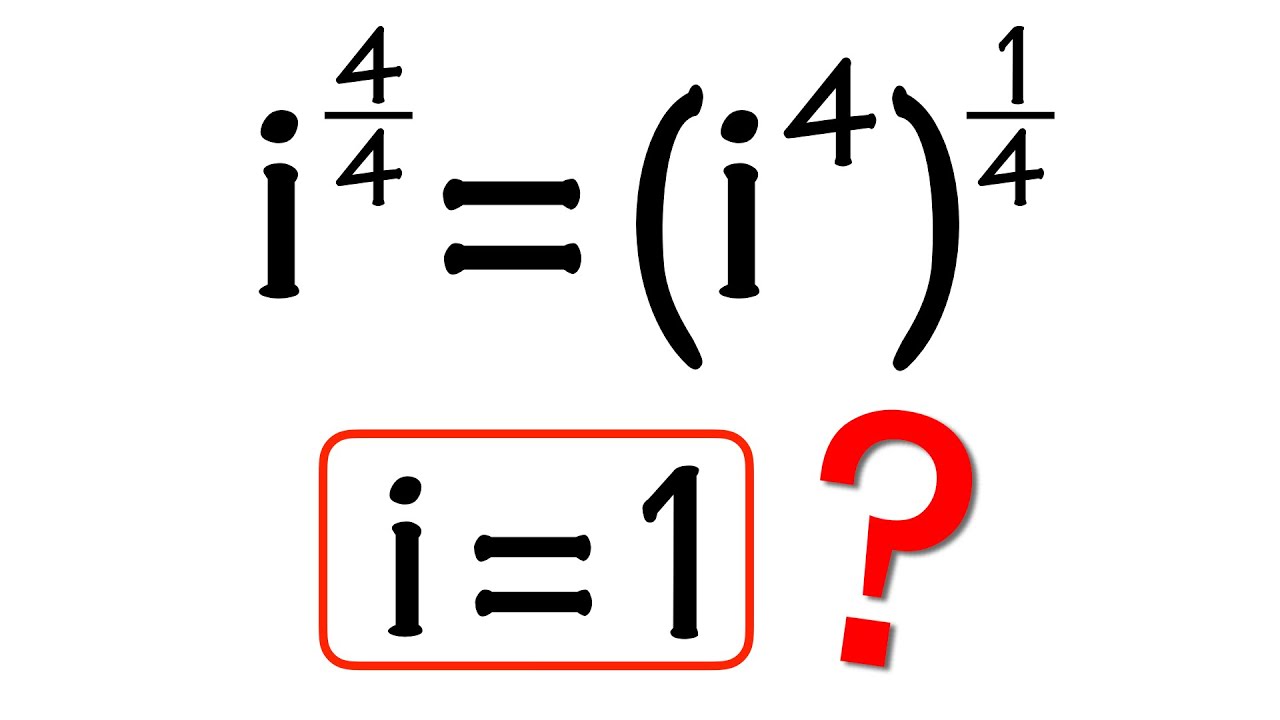
Показать описание
The powers of the imaginary unit i are always intriguing. Here we will examine i^(4/4). Is the result 1 or i? We have to be careful when an imaginary number is raised to a fractional power!
0:00
0:06 is i = 1?
4:23 (i^4)^(1/4) vs (i^(1/4))^4
10:14 (i^3)^(1/4) vs (i^(1/4))^3
13:53 summary on z^(m/n)
15:41 check out Brilliant to learn more!
16:35 bonus part
---------------------------------------------------------------------------------------------------
***Thanks to ALL my lovely patrons for supporting my channel and believing in what I do***
AP-IP Ben Delo Marcelo Silva Ehud Ezra 3blue1brown Joseph DeStefano
Mark Mann Philippe Zivan Sussholz AlkanKondo89 Adam Quentin Colley
Gary Tugan Stephen Stofka Alex Dodge Gary Huntress Alison Hansel
Delton Ding Klemens Christopher Ursich buda Vincent Poirier Toma Kolev
Tibees Bob Maxell A.B.C Cristian Navarro Jan Bormans Galios Theorist
Robert Sundling Stuart Wurtman Nick S William O'Corrigan Ron Jensen
Patapom Daniel Kahn Lea Denise James Steven Ridgway Jason Bucata
Mirko Schultz xeioex Jean-Manuel Izaret Jason Clement robert huff
Julian Moik Hiu Fung Lam Ronald Bryant Jan Řehák Robert Toltowicz
Angel Marchev, Jr. Antonio Luiz Brandao SquadriWilliam Laderer Natasha Caron Yevonnael Andrew Angel Marchev Sam Padilla ScienceBro Ryan Bingham
Papa Fassi Hoang Nguyen Arun Iyengar Michael Miller Sandun Panthangi
Skorj Olafsen Riley Faison Rolf Waefler Andrew Jack Ingham P Dwag Jason Kevin Davis Franco Tejero Klasseh Khornate Richard Payne Witek Mozga Brandon Smith Jan Lukas Kiermeyer Ralph Sato Kischel Nair
---------------------------------------------------------------------------------------------------
Комментарии
 0:17:35
0:17:35
 0:00:43
0:00:43
 0:00:37
0:00:37
 0:00:23
0:00:23
 0:00:52
0:00:52
 0:01:24
0:01:24
 0:00:31
0:00:31
 0:00:17
0:00:17
 0:40:57
0:40:57
 0:00:43
0:00:43
 0:00:41
0:00:41
 0:00:59
0:00:59
 0:00:05
0:00:05
 0:01:00
0:01:00
 0:00:46
0:00:46
 0:00:16
0:00:16
 0:00:13
0:00:13
 0:00:37
0:00:37
 0:00:09
0:00:09
 0:01:00
0:01:00
 0:00:17
0:00:17
 0:00:45
0:00:45
 0:20:17
0:20:17
 0:00:10
0:00:10