filmov
tv
Entrance examination to Stanford University

Показать описание
What do you think about this question? If you're reading this ❤️. Have a great day!
Hello My Friend ! Welcome to my channel. I really appreciate it!
@higher_mathematics
#maths #math
Hello My Friend ! Welcome to my channel. I really appreciate it!
@higher_mathematics
#maths #math
Entrance examination to Stanford University
Can you Pass Stanford University Entrance Exam ?
Entrance examination to Stanford University
Entrance examination to Stanford University
Entrance examination to Stanford University
Entrance examination to Stanford University
Entrance examination to Stanford University
Entrance examination to Stanford University
Spain|| A Nice algebra problem from Stanford University Entrance exam
Entrance examination to Stanford University
Entrance examination to Stanford University
Entrance examination to Stanford University
Entrance examination to Stanford University
Entrance examination to Stanford University
Entrance examination to Stanford University
Stanford University Entrance Interview || Can you Really Pass Admission Exam ?
A very tricky Question from Stanford University Entrance Exam | Find the Value of a=? & b=?
Stanford University Entrance Aptitude Test Advanced tricks
Entrance examination to Stanford University
Stanford Entrance Exam-HOW TO FIND OC? You Qualified?
Stanford University Entrance Exam | x^4−12x−5=0
The Five Words That Helped Me Get Into Stanford
How to get into Stanford + EXACTLY what Stanford looks for (GPA, Scores, Extracurriculars, Essays)
Could You Get Into Stanford? Admission Test From 1892
Комментарии
 0:12:28
0:12:28
 0:15:33
0:15:33
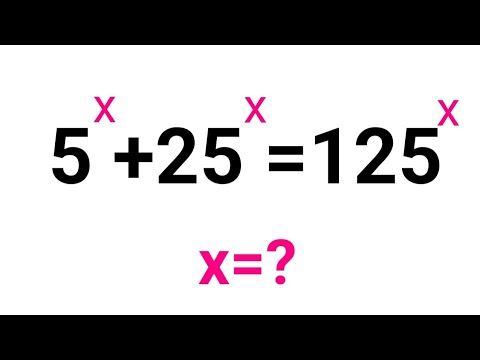 0:13:12
0:13:12
 0:11:05
0:11:05
 0:11:19
0:11:19
 0:10:34
0:10:34
 0:10:50
0:10:50
 0:10:54
0:10:54
 0:09:24
0:09:24
 0:12:04
0:12:04
 0:11:21
0:11:21
 0:11:23
0:11:23
 0:12:26
0:12:26
 0:12:08
0:12:08
 0:11:05
0:11:05
 0:10:24
0:10:24
 0:15:34
0:15:34
 0:23:15
0:23:15
 0:06:09
0:06:09
 0:05:12
0:05:12
 0:21:08
0:21:08
 0:00:27
0:00:27
 0:10:03
0:10:03
 0:04:54
0:04:54