filmov
tv
Evaluating a Radical Expression

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Radicals
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #Radicals
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Evaluating a Radical Expression
How To Simplify Radicals
Simplifying Radicals Easy Method
How to evaluate radical expression if x is nested radical? | Olympiad Math
Evaluating a Radical Expression in Three Ways
Evaluating A Radical Expression | Two Ways
Learn to add and subtract radical expressions
Simplify a radical expression with variables
Evaluating a Radical Expression
Evaluating a Radical using a Radical Expression
How to evaluate a radical function given three different values
Evaluating A Radical Expression in Two Ways
Learn how to simplify a radical
Fractional Exponents
Evaluating A Radical Expression with Cardano's Formula
Solving Radical Equations
Evaluate the Radical Expression | NO CALCULATORS ALLOWED
Let's Evaluate a Radical Expression
Evaluating A Radical Expression | Two Methods
Simplifying a radical expression using rational exponents
Nice Radical Expression Simplification | Math Olympiad Algebra Problem | Caluculators NOT allowed
How to Simplify Radicals (NancyPi)
Learn how to evaluate an expression with the radical of a perfect square ex 2, 5root(36)
Evaluating A Radical Expression
Комментарии
 0:05:14
0:05:14
 0:13:14
0:13:14
 0:03:42
0:03:42
 0:04:55
0:04:55
 0:08:45
0:08:45
 0:08:38
0:08:38
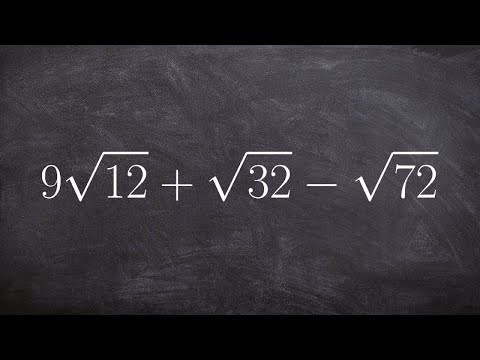 0:03:41
0:03:41
 0:05:14
0:05:14
 0:08:13
0:08:13
 0:01:43
0:01:43
 0:02:26
0:02:26
 0:09:22
0:09:22
 0:04:09
0:04:09
 0:11:32
0:11:32
 0:11:49
0:11:49
 0:17:11
0:17:11
 0:03:16
0:03:16
 0:08:52
0:08:52
 0:09:13
0:09:13
 0:04:26
0:04:26
 0:13:11
0:13:11
 0:17:51
0:17:51
 0:02:27
0:02:27
 0:00:33
0:00:33