filmov
tv
Expanding and Condensing Logs
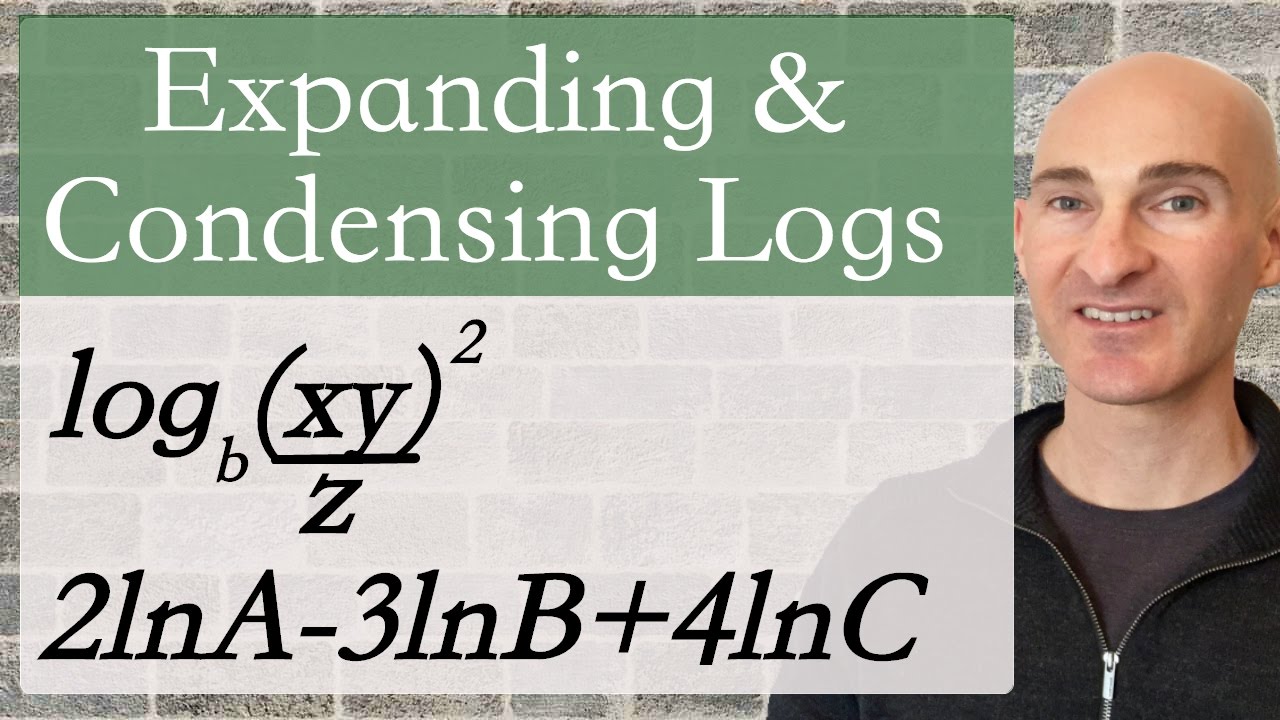
Показать описание
Learn how to Expand and Condense Logs in this free math video tutorial by Mario's Math Tutoring. We go through the expanding and condensing formulas for logs as well as some example problems.
0:15 Properties of logs for expanding and condensing
1:52 Expanding Logs examples
6:25 Condensing Logs examples
Get the worksheet above from my TpT store. 10 expanding and 10 condensing problems utilizing the product, quotient and power properties. Answer key is also provided.
* Organized List of My Video Lessons to Help You Raise Your Scores & Pass Your Class. Videos Arranged by Math Subject as well as by Chapter/Topic. (Bookmark the Link Below)
0:15 Properties of logs for expanding and condensing
1:52 Expanding Logs examples
6:25 Condensing Logs examples
Get the worksheet above from my TpT store. 10 expanding and 10 condensing problems utilizing the product, quotient and power properties. Answer key is also provided.
* Organized List of My Video Lessons to Help You Raise Your Scores & Pass Your Class. Videos Arranged by Math Subject as well as by Chapter/Topic. (Bookmark the Link Below)
Expanding and Condensing Logarithms (Explained Step by Step)
Expanding Logarithmic Expressions
Expanding and Condensing Logs
Condensing Logarithmic Expressions
Learn how to condense logarithmic expression to one log
Learn the basics for expanding and condensing a logarithmic equation
Expanding and Condensing Logs
Expanding logarithmic expressions
Expanding and Condensing Logarithmic Expressions A
How to Expand and Condense Logarithms ( Basic Log Rules )
How to Expand Logarithms (Precalculus - College Algebra 59)
Logs Complete Guide to Mastering Logarithms - Rewrite, Evaluate, Expand, Condense, Graph, Solve
Expanding and Condensing Logarithmic Expressions (harder examples)
Expanding logarithmic expressions
Logarithms Part 3: Properties of Logs, Expanding Logarithmic Expressions
Expanding and Condensing a logarithmic expression
Logarithms Expanding and Condensing
Learn to condense logarithmic expressions to one single logarithm
Expanding and Condensing Logarithms
Properties Of Logarithms Expanding and Condensing
0E Expanding and Condensing Logarithms
Expanding and Condensing Logarithms
Expanding and Condensing Logarithms
Expanding and Condensing Logarithms
Комментарии
 0:12:37
0:12:37
 0:04:36
0:04:36
 0:09:14
0:09:14
 0:03:43
0:03:43
 0:01:53
0:01:53
 0:00:43
0:00:43
 0:04:31
0:04:31
 0:03:54
0:03:54
 0:04:44
0:04:44
 0:23:26
0:23:26
 0:28:42
0:28:42
 0:51:02
0:51:02
 0:07:59
0:07:59
 0:01:33
0:01:33
 0:07:06
0:07:06
 0:07:24
0:07:24
 0:10:24
0:10:24
 0:03:21
0:03:21
 0:10:55
0:10:55
 0:20:21
0:20:21
 0:13:01
0:13:01
 0:05:29
0:05:29
 0:28:49
0:28:49
 0:09:03
0:09:03