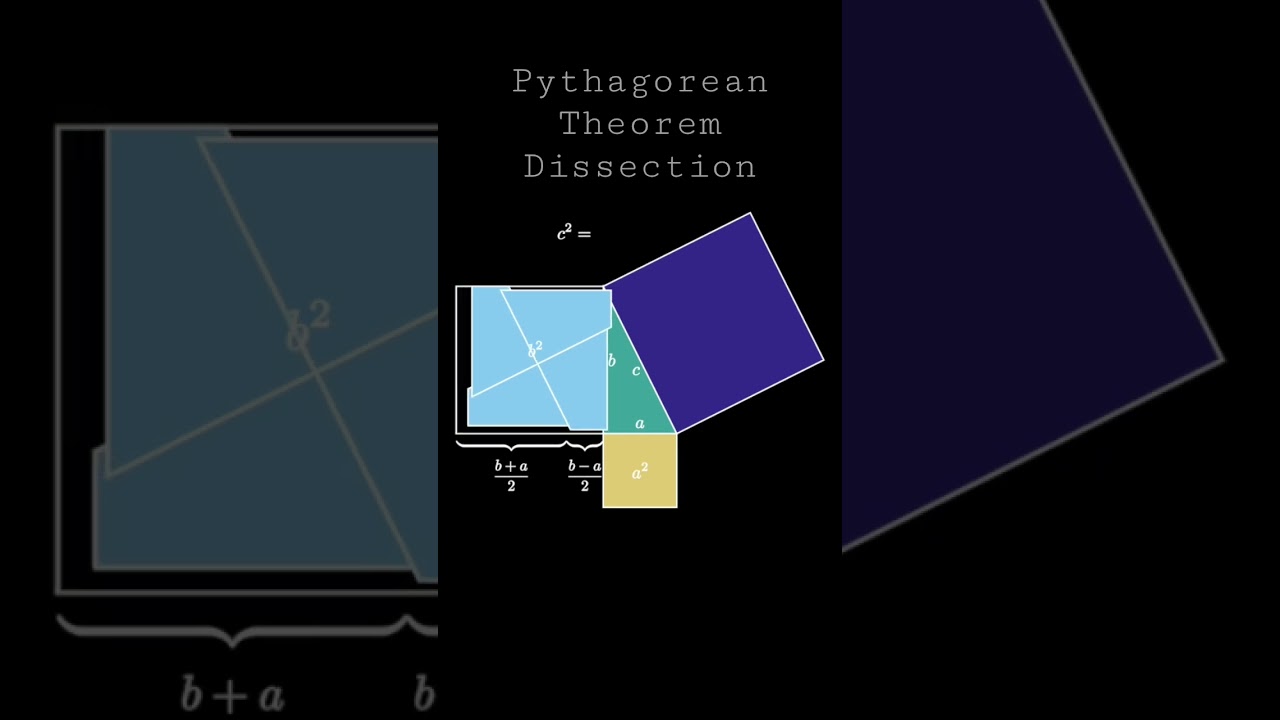
Pythagorean Theorem XI (Dudeney’s Dissection)

This is a short, animated visual proof of the Pythagorean theorem (the right triangle theorem) using a Henry Dudeney's dissection argument (congruent-by-addition proof).

This animation is based on a proof from Henry Dudeney and is discussed in Howard Eve's book "Great Moments in Mathematics (before 1650)." You can also find this in Roger Nelsen's first PWW compendium on page 6.

For other proofs of this same fact check out:

#math #manim #pythagoreantheorem #pythagorean #triangle #animation #theorem #pww #proofwithoutwords #visualproof #proof #mathshorts #mathvideo

To learn more about animating with manim, check out:

[asparkdeity]

That’s a really nice dissection :D I wrote the maths behind it for another comment, I’ll paste it here so ppl can see why the dissection of
b = (b-a)/2 + (b+a)/2 is key.


I won’t go into full details on the calculation. The area of 4 quadrilaterals (I’ll call the distinct shape Q) in this construction + a^2 = c^2, we want to see why this is.

But I think this is the mathematical idea: see where the two lines inside the square meet? They intersect at the centre of the square by the symmetry of the construction, at (b/2, b/2).

Now drop the perpendicular from the centre to each of the 4 edges of the square. We see now that each perpendicular dissects each of the four Q into a smaller right-angled triangle (base (b+a)/2 - b/2 = a/2, height b/2) and a smaller trapezium (lengths b/2 and (b-a)/2, height b/2).

Hence, we can find out the area of 4Q by adding the trapezium and triangle areas for each Q. Furthermore, we can find the area of 4Q in terms of c using similarity, because notice how the lengths of the mini right-angled triangles are a/2, b/2 and the corresponding lengths of the original right-angled triangle are a, b ==>
length of hypotenuse of small triangle = length of slanting edge of Q = c/2. This means the length of each line inside the square is in fact c! This is the key observation for this proof.

Now split up Q the square into two rectangles, by dropping a perpendicular from where one of the two lines inside the square meets it’s edge, all the way to the opposite edge of the square; this splits the square into two rectangles, one of lengths (a+b)/2 and b, the other lengths (a-b)/2 and b. U can split the bigger rectangle into a right angled triangle and trapezium, and u’ll see this right angled triangle is a carbon copy of the original triangle! Hence u have found a way to compute the area of the square, b^2, in terms of a and c. Hence compute the area of the square I.e. the area of 4Q in both these different ways, equate the areas and simplify down and u should get that the area of 4Q = b^2 = c^2 - a^2, which is precisely the result in the video!

[richardgratton]

It’s not clear to me why the sides of the b x b square are divided into (b + a)/2 and (b-a)/2. Can I someone explain it to me?

[TheDigiWorld]

Really nice video, but personally I really find the square inside a square proof as the easiest to understand

[mihailmilev]

I'm glad Dudeney got his life together and became a mathematician after Harry left to Hogwarts

[nm_]

Can u do a full length video of this proof with more details?

[ralf_]

why is Phythagoream Theorem still called a "Theroem" when it's already proofn that it will apply to the real world, shouldn't it be called Phythagoream Law or something similar?

[VishritiMishra]

bro i need a god damn teacher like that i m a 4th grader and i actaully understand that

[uri]

Lacking all the geometrical-reasoning steps that are necessary to justify the “visual” assertions and, in particular, comparing this “visual proof” to the many well-established visual proofs of the Pythagorean theorem, at best this is no more than a visual demonstration of the relationship the theorem describes. For example, expand (b-a)/2 + (b+a)/2 and get b/2 – a/2 + b/2 + a/2. Regardless of the value of a, -a/2 and +a/2 cancel each other. And then 2 x b/2 = b regardless to the value of b. And why are the 2 copies of c do not intersect the b sides at a right angle? Because then c would be equal to b. In their comments, @asparkdeity8717 and @McGravyboat show this visual demonstration is far from being a complete proof.

[DebKarmakar-ztxo]

Sir what is the factorial of infinity ♾️

[ravsuri]

Is this really a proof? It is not clear to me why the side lengths are cut that way or why the leftover piece has length 'a'. Such demonstrations make one ask: what does it mean to prove something.

[hananebabaali]

It really a good proof but it kinda complicated for me 😅

[comicrelief]

Does this convince you absolutely of the theorem?

[ddichny]

"You can check that the side length is A" - Then maybe you should do that in the video? Or is this proof via "trust me bro"?