filmov
tv
An Interesting Rational Expression
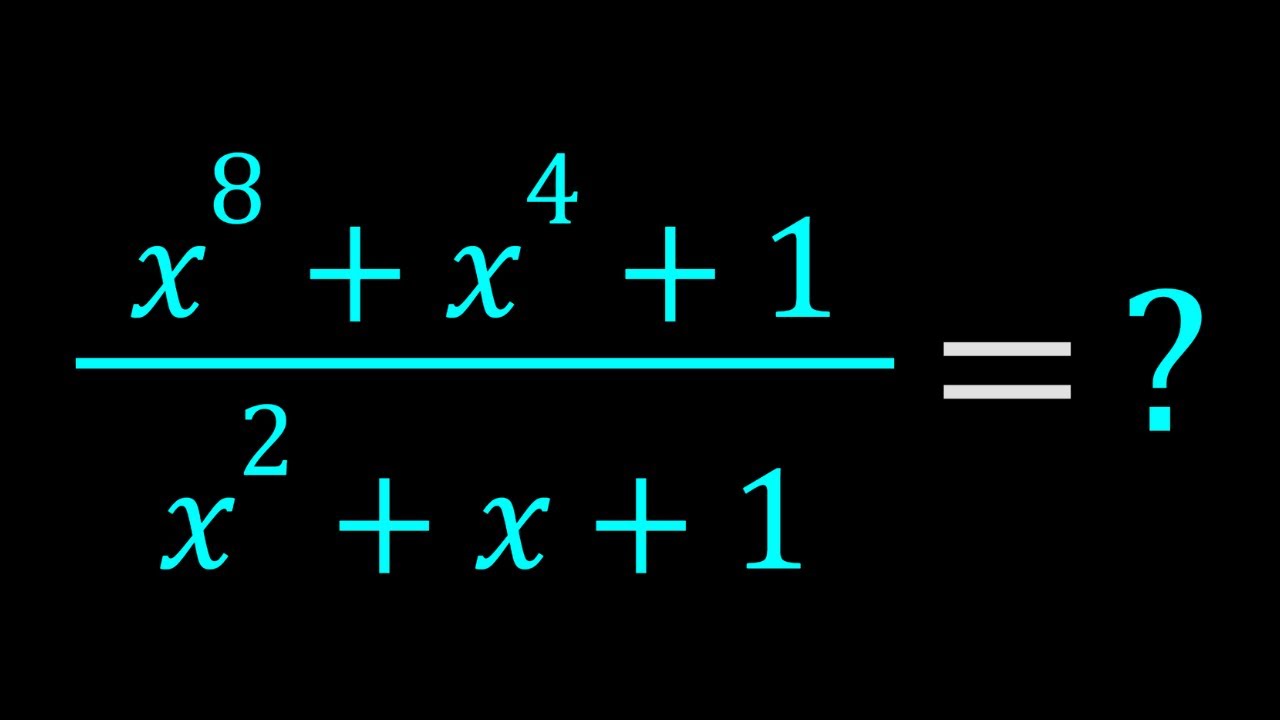
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
INFINITE SERIES:
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
INFINITE SERIES:
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
An Interesting Rational Expression
Simplifying Rational Expressions
Rational Expressions - Basic Introduction
Rational Expression tips
Simplifying rational expressions introduction | Algebra II | Khan Academy
What are rational expressions
How to Simplify Rational Expressions in Algebra
Simplifying Complex Rational Expressions
Binomial Theorem-Finding the Constant Term
Manipulating Rational Expressions: Simplification and Operations
Simplifying Rational Expressions... How? (NancyPi)
Solving Rational Equations Easier Method
Solving Rational Equations
06 - Simplifying Rational Expressions in Algebra, Part 1
Simplifying Rational Algebraic Expressions (RAE) - Grade 8 Math
How to simplify a rational expression using factoring
How to Simplify Rational Expressions
Simplifying Rational expressions
Fun Rational Equation
Multiplying Rational Expressions
Add and Subtract Rational Expressions Step by Step
14 - Multiplying, Dividing & Simplifying Rational Expressions, Part 1
Simplifying a complex rational expression
Structure in rational expression | Polynomial and rational functions | Algebra II | Khan Academy
Комментарии
 0:09:48
0:09:48
 0:11:08
0:11:08
 0:12:46
0:12:46
 0:19:28
0:19:28
 0:07:28
0:07:28
 0:02:36
0:02:36
 0:01:00
0:01:00
 0:12:46
0:12:46
 0:00:54
0:00:54
 0:09:30
0:09:30
 0:14:04
0:14:04
 0:04:33
0:04:33
 0:11:03
0:11:03
 0:37:43
0:37:43
 0:08:33
0:08:33
 0:01:30
0:01:30
 0:00:59
0:00:59
 0:03:29
0:03:29
 0:01:32
0:01:32
 0:12:05
0:12:05
 0:12:52
0:12:52
 0:26:55
0:26:55
 0:02:55
0:02:55
 0:04:41
0:04:41