Derivation of the one dimensional wave equation using partial derivatives of the wave function.

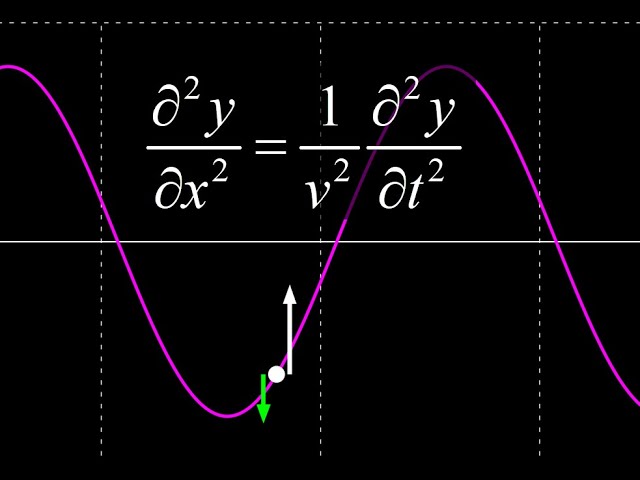
01:13 Time derivatives of the wave function: we begin with an animation of a spot oscillating on the string. Because this is a transverse wave, the oscillation of the spot is purely vertical when the wave velocity is horizontal, and this oscillation is simple harmonic. The velocity and acceleration vectors are shown in the animation of the oscillating spot, and our first goal is to compute the velocity of a point on a string and the acceleration of a point on a string by using the partial derivatives of the wave function with respect to time. We introduce the del notation for partial derivatives and take the first and second partial derivatives to get the velocity and acceleration of the string as the wave passes through it.

02:49 The second time derivative is proportional to the wave function itself! Taking two derivatives of a sinusoidal function yields a familiar result: the second derivative is proportional to the original function. This is the key result from our calculation of partial time derivatives.

03:28 x derivatives of the wave function: next, we turn our attention to computing x derivatives of the wave function. The first partial with respect to x is the slope of the string, and the second partial derivative with respect to x is the curvature or concavity of the string. Again we find the important result that the second derivative with respect to x yields a function that is proportional to the original wave function.

04:56 The one dimensional wave equation: solving for y(x,t) in both of our second partial derivatives and setting them equal, we obtain the famous second order partial differential equation describing the motion of a wave on a string: the one-dimensional wave equation!

06:08 Note on concavity and the sign of acceleration: we note that the 1D wave equation tells us that when the concavity of the string is positive, so is the acceleration (and vice versa). Why should this be true? We zoom in on a spot on the string in a region of upward concavity and see that the tension pulling up and to the right lies at a steeper angle than the tension pulling down and to the left, because the slope of the string is getting steeper as we go to the right. This means the upward y component of force outweighs the downward y component of force, causing an upward acceleration. This more fundamental reasoning is precisely what we need to derive the wave equation directly from Newton's second law, which is the subject of the next video.