filmov
tv
Real Analysis | Sequential limits in functions.
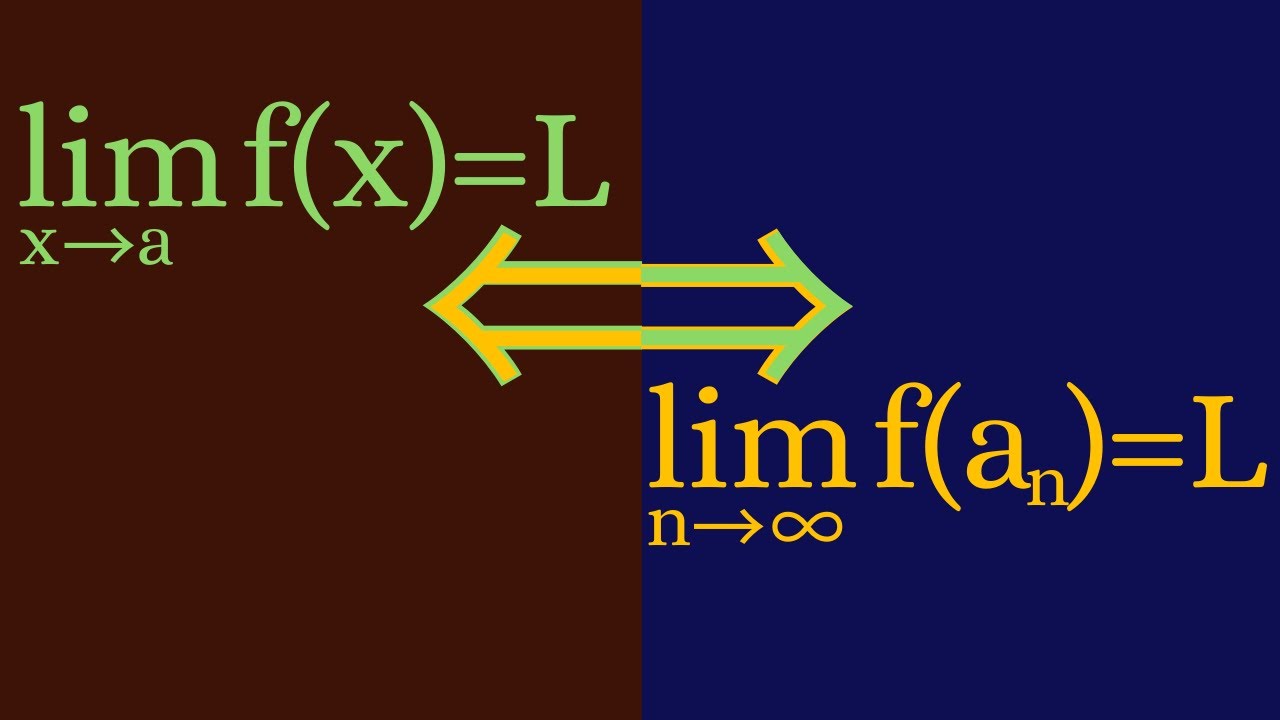
Показать описание
We prove a nice result that allows us to use technique of limits of sequences to approach limits of functions.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
Definition of the Limit of a Sequence | Real Analysis
Connecting Function Limits and Sequence Limits | Real Analysis
Real Analysis | Sequential limits in functions.
Proof: Sequence (3n+1)/(n+2) Converges to 3 | Real Analysis
Converging and Diverging Sequences Using Limits - Practice Problems
Proof: The Limit of a Sequence is Unique | Real Analysis
Sequential Characterization of Limits of a Function of a Real Variable
Limit of a Sequence by Epsilon definition (Hard example)
Real Analysis | Limit of a Sequence | Convergence and Divergence Of Sequence
Proving All the Sequence Limit Laws | Real Analysis
Limit Points (Sequence and Neighborhood Definition) | Real Analysis
Limit of a Sequence | Difference between Limit and Limit Point | Sequence of real numbers: 05
Real Analysis 9 | Subsequences and Accumulation Values
❖ Finding the Limit of a Sequence, 3 more examples ❖
Proof: Sequence (n+1)/n Converges to 1 | Real Analysis
Sequences that Diverge to Infinity (Definition) | Calculus, Real Analysis
Real analysis | limit of sequence definition and examples | difference between limit and limit point
limit of a sequence real analysis | limit of sequence | bsc msc csir net iit jam
Epsilon-Delta Definition of Functional Limits | Real Analysis
Sequence and Real sequence . #maths #realanalysis
Real Analysis Course #18 - Sequence Limits are Unique Proof
UPSC Mathematics Real Analysis | Lecture 30 - Limits Definition and Sequential Criterion
limit of a sequence# Real Analysis-I
Sequential Criterion for Limits of Functions
Комментарии
 0:13:59
0:13:59
 0:12:22
0:12:22
 0:19:44
0:19:44
 0:06:53
0:06:53
 0:30:13
0:30:13
 0:13:22
0:13:22
 0:06:18
0:06:18
 0:09:52
0:09:52
 0:18:36
0:18:36
 0:54:07
0:54:07
 0:11:36
0:11:36
 0:22:44
0:22:44
 0:08:18
0:08:18
 0:03:24
0:03:24
 0:06:43
0:06:43
 0:09:59
0:09:59
 0:37:12
0:37:12
 0:18:51
0:18:51
 0:21:38
0:21:38
 0:00:11
0:00:11
 0:05:35
0:05:35
 0:31:39
0:31:39
 0:10:38
0:10:38
 0:18:31
0:18:31