filmov
tv
Find all real pairs (x,y)

Показать описание
This is a competition problem from Russia. Kindly share alternative strategies to the one I used if there are. I am also not sure if there are other solutions.
Find all real pairs (x,y)
How to find Integers pairs (x,y) for this equation ?
Finding Ordered Pairs that Satisfy a Given Equation
Finding Mind Boggling Real Pairs (x,y) || A Hard System of Non-Linear Algebraic Equations || AMS
Find all pairs of integers (x, y) such that x^3+y^3=(x+y)^2. Math Olympiad Challenges
Sketch the Set of All Ordered Pairs (x, y) with x = 3
Sketch the set of all ordered pairs (x, y) with x less than or equal to zero
Ordered Pairs (x+y,2) and (4,x-y) are equal, Find x and y.
Geometry: Dilation,Scale Factor,Ratio #maths#mathematics #science #mathshack #education #mathskills
Sketch the set of all ordered pairs (x, y) such that x^2 + y^2 is less than or equal to 1
Find all ordered pairs of real numbers that satisfy both the equations `x^2 +y^2=2 xy` and `x^2...
Determine Which Ordered Pairs are a Solution to the Equation
Find all 6 pairs of solutions
x + y = xy, integral pairs of (x, y) | Equations & Numbers | Q58 CAT 2004 Quant Solution
A nice algebra puzzle: Find all pairs of x and y
The number of ordered pairs (x,y) satisfying 3x+2y=27 is a, then find the value of a,if x and y are
Maths for everyone No 35 - All the pairs (x , y) such that x + y = x. y
Find All Pairs Of Non-Negative Integers (X,Y) | Math Olympiad | (x+y)^6-30y=x
How to Find Ordered Pairs of a Relation
Array : Find all pairs (x, y) in a sorted array so that x + y z
Find All Pairs Of Non Negative Integers X,Y | 2^x+1=y^2 | Math Olympiad
The number of all possible ordered pairs `(x, y), x, y in R` satisfying the system of equations `
DLE Preparation Class||Class - 8||Ordered Pairs||Optional Math||Find the values of x and y|| Model Q
Find number of all pairs of real number (x,y) for which x^2+y^2+xy=133 and x+y+√xy=19
Комментарии
 0:14:38
0:14:38
 0:06:45
0:06:45
 0:02:53
0:02:53
 0:07:56
0:07:56
 0:10:34
0:10:34
 0:01:44
0:01:44
 0:01:16
0:01:16
 0:03:59
0:03:59
 0:30:53
0:30:53
 0:03:19
0:03:19
 0:02:56
0:02:56
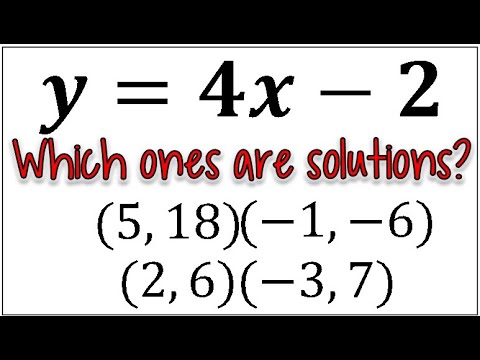 0:04:13
0:04:13
 0:12:22
0:12:22
 0:02:43
0:02:43
 0:05:20
0:05:20
 0:01:49
0:01:49
 0:11:34
0:11:34
 0:05:28
0:05:28
 0:03:47
0:03:47
 0:01:29
0:01:29
 0:04:37
0:04:37
 0:02:20
0:02:20
 0:03:56
0:03:56
 0:13:05
0:13:05