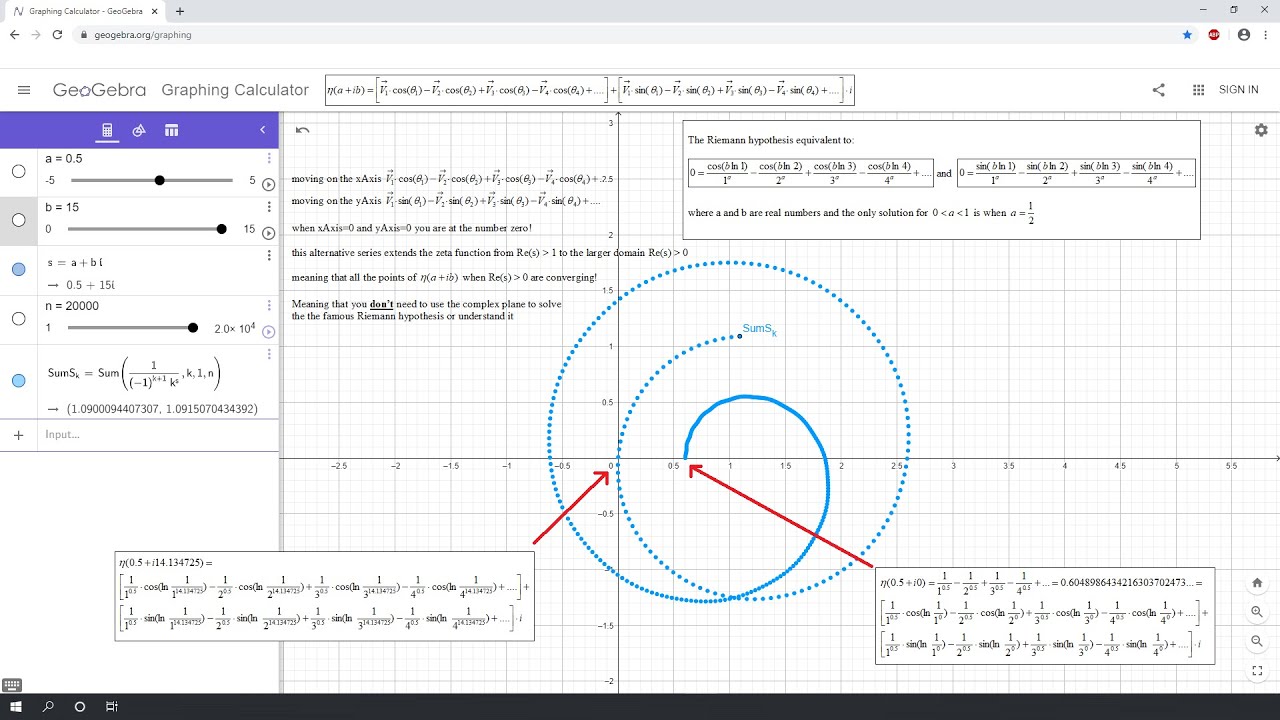
Removing the Riemann Hypothesis from the Complex Plane

preview_player
Показать описание
in this chapter I will show how you can removing the Riemann hypothesis from the complex plane
meaning that you can show the same idea using only real number plane without using analytic continuation
  1. Isaac Mor
  2. Riemann Hypothesis
  3. Riemann zeta
  4. Zeta Function
  5. Analytic Continuation
  6. Critical Line
Рекомендации по теме
Removing the Riemann 0:05:28

Removing the Riemann Hypothesis from the Complex Plane

May we shift 0:01:38

May we shift critical line in Riemann hypothesis to left by removing 1/2^s from the equation?

But what is 0:22:11

But what is the Riemann zeta function? Visualizing analytic continuation

RIEMANN HYPOTHESIS PROOF 0:05:41

RIEMANN HYPOTHESIS PROOF / SOLVED, 33262 VIEWS, 0 COUNTEREXAMPLE! (M2) #riemannhypothesis

The Proof of 0:10:54

The Proof of Riemann Hypothesis Through Zeta Universality Theorem

A discussion on 0:01:42

A discussion on the Zeta function | Properties | Riemann's Hypothesis

Step Zero of 0:10:41

Step Zero of Analytic Continuation Gateway to the Riemann Hypothesis #mathmatics

Proof of the 0:03:17

Proof of the Riemann Hypothesis

True answer to 0:02:04

True answer to the Riemann hypothesis

How to Prove 0:09:39

How to Prove the Riemann Hypothesis

Carlos Castro Perelman 1:33:58

Carlos Castro Perelman - On the Riemann Hypothesis and Complex Scalings

The Riemann Hypothesis 0:12:48

The Riemann Hypothesis and the secret of prime numbers - CHAPTER 1

The Riemann Hypothesis 0:01:31

The Riemann Hypothesis

Riemann hypothesis 0:02:27

Riemann hypothesis

Towards Riemann Hypothesis 0:14:19

Towards Riemann Hypothesis

The Basel Problem 0:58:32

The Basel Problem Part 2: Euler's Proof and the Riemann Hypothesis

The Riemann Hypothesis 0:17:43

The Riemann Hypothesis - Picturing The Zeta Function

A Direct Proof 0:25:44

A Direct Proof of the Riemann Hypothesis - Part 1: Background on the Riemann Zeta Function

Primes in arithmetic 1:31:14

Primes in arithmetic progressions: The Riemann Hypothesis - and beyond! - James Maynard

11b - Riemann 0:23:25

11b - Riemann Zeta Function Has Only One Pole

My proof of 0:07:56

My proof of Riemann Hypothesis

De Branges Spaces 1:31:00

De Branges Spaces - Lecture 16 - The Riemann Hypothesis

Riemann Hypothesis stands 0:27:59

Riemann Hypothesis stands proved, what next?

My Riemann hypothesis 0:45:08

My Riemann hypothesis proof fixes current mathematics

Комментарии
Автор

Isaac, how are you doing? Thanks for the pointer to your videos. I also enjoyed some of your colored fractals, they look cool.
I think that Jeff does not like me, and he will be fine with it.
About your argument around 0:50 for the identity between eta and zeta, we are clear that it only works for Re(s) > 1, right? For Re(s) > 0 there is more required. Will this be explained in one of the next videos?

tommyrjensen
Автор

I have reached that point too at your equations at 4:13 where i have two equations with two unknowns to solve, i made all sin terms into cos and im on a way to proceed and combine all cos terms as one with the b term, im trying to show that since b has many values then a = 1/2 has to be the only answer and if not then Riemann's hypothesis its not true!

TruthOfZ
Автор

If the proof can succeed, then this is the proof by contradiction, which leads to the desired result. As long as the assumption is still unproven, as long as the uniqueness is attainable. However, I suspect that this assumption has long since been proven and no one has noticed.

michaelkoch