Geometry :INTERESTING PROBLEM -In triangle ABC given that AD perpendicular to BC. Prove that AB=2DE.

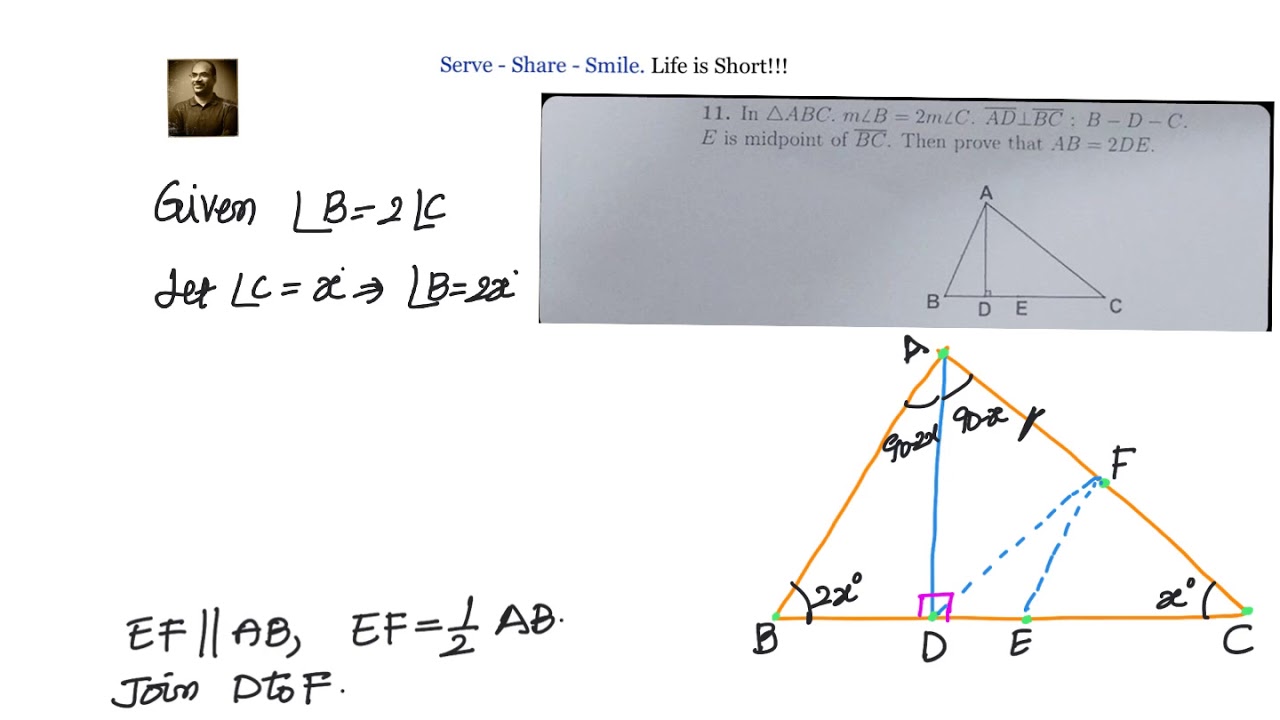
Geometry : In triangle ABC, AD perpendicular to BC. E is midpoint of BC.
If angle B is twice angle C then prove that AB = 2 DE.

Concept used:
1) Mid point theorem
2) Circumcenter of right triangle is midpoint of hypotenuse.

Solution steps:
1) Let F be midpoint of AC. Join D and E to F. Given E is midpoint of BC.
2) By midpoint theorem, EF = 1/2 AB and EF is parallel to AB.
3) Let angle c be x, then angle B is equal to 2x.
4) In right triangle ADC, F is Circumcenter. So, AF = DF.
5) Now, after finding values of all the angles of the triangles ADB, ADC and DEF, we
find that DEF is an isosceles triangle.
6) DE = EF, so AB = 2 DE.

Be safe ❤️🙏🏼

[gurjotkaur]

Omg I'm so grateful to you!! I was struggling on this problem for so long, thank you so much 🤍🤍🤍🤍