filmov
tv
Trigonometric integrals - sin^mcos^n, m and n even (KristaKingMath)
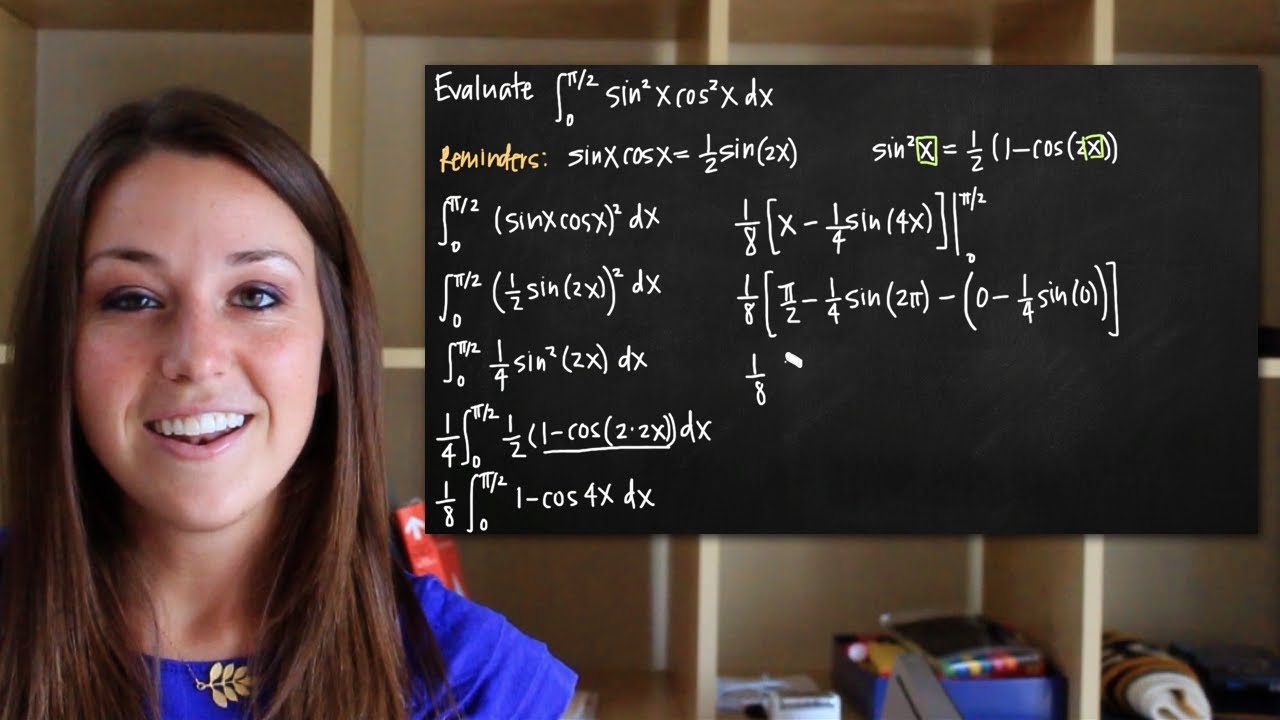
Показать описание
Learn how to find the integral of the product of a higher order sine function and higher order cosine function. In this particular example, we'll talk about the method for finding the integral when sine and cosine are even
● ● ● GET EXTRA HELP ● ● ●
● ● ● CONNECT WITH KRISTA ● ● ●
Hi, I’m Krista! I make math courses to keep you from banging your head against the wall. ;)
Math class was always so frustrating for me. I’d go to a class, spend hours on homework, and three days later have an “Ah-ha!” moment about how the problems worked that could have slashed my homework time in half. I’d think, “WHY didn’t my teacher just tell me this in the first place?!”
Trigonometric integrals - sin^mcos^n, m and n even (KristaKingMath)
Trigonometric integrals - sin^mcos^n, odd n (KristaKingMath)
Trigonometric integrals - sin^mcos^n, odd m (KristaKingMath)
Integral of the form sin^m cos^n
How to solve integral sin^m(x) cos^n(x) dx using u-sub (n odd) // trigonometric integral, trig int
Integrals of Sin^mx Cos^nx When Both M and N are Even
Trig Integral with Sin^m*cos^n (m and n both even)
trig integrals involving sine and cosine (calculus 2)
Trig Integration with Only Even Powers
Trig Integral problem with Sin^m*cos^n form
How to integrate sin^m cos^n
Integrating Even Powers of sin(x) and cos(x)
Integration of (sin^m cos^n) and (sec^m tan^n)
Trigonometric Integrals --- ∫sin^n(x)cos^m(x)dx via Pythagorean or Half-Angle Identities
Integrals of trigonometric functions, sin(mx)sin(nx) (KristaKingMath)
Calculus 2: Integration of Trig Fcts (16 of 16) Integral of [sin^m(x)][cos^n(x)]=? General Approach
Trigonometric Integrals: Guidelines for sin(x)cos(x)
Integration of a product of sin^m x cos^n x
Lecture 15: Trigonometric Integrals | Calculus II
How to calculate the integral of (Cos x)^n
Reduction Formula 04(sin^m cos^n)
Reduction Formula sin^mx.cos^nx
Trigonometric Integration 1: sine, cosine and their combination.
Integrals of Sin^mx Cos^mx When M and N are Even & Odd
Комментарии
 0:07:34
0:07:34
 0:11:20
0:11:20
 0:10:14
0:10:14
 0:09:05
0:09:05
 0:03:17
0:03:17
 0:08:55
0:08:55
 0:14:09
0:14:09
 0:15:42
0:15:42
 0:08:37
0:08:37
 0:09:39
0:09:39
 0:10:03
0:10:03
 0:04:28
0:04:28
 0:17:37
0:17:37
 0:08:10
0:08:10
 0:04:30
0:04:30
 0:03:40
0:03:40
 0:07:59
0:07:59
 0:06:18
0:06:18
 1:29:43
1:29:43
 0:08:52
0:08:52
 0:05:10
0:05:10
 0:11:51
0:11:51
 0:19:13
0:19:13
 0:09:32
0:09:32