Properties of GCD || Lesson 125 || Discrete Math & Graph Theory || Learning Monkey ||

Properties of GCD
In this class, We discuss the Properties of GCD.
The reader should have prior knowledge of GCD using Euclidean algorithms. Click here.
If GCD of a and b is. Then we have integers u and v such that au + bv = 1.
The other way we write the definition
If a, b, u, and v are integers such that au + bv = 1, then GCD(a, b) = 1
Proof:
Assume “t” is GCD(a, b)
We can write a = tk and b = tl for some integers k, l.
Given 1 = au + bv
1 = tku + tlv
1 = t(ku + lv)
The above equation happens: t divides 1.
So t value is {-1, 1}
GCD = t = 1.
Property 2:
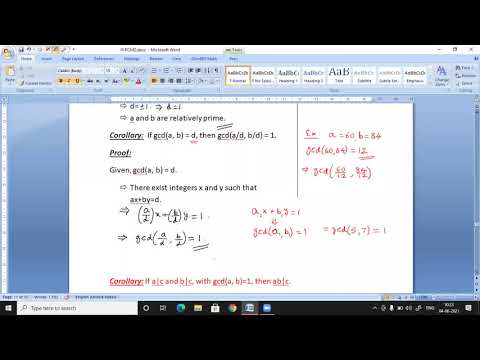
If c | ab and GCD(a, c) = 1, then c | b.
Given GCD(a, c) = 1, we have integers u and v such that ua + vc = 1.
Multiply by b.
uab + vbc = b
Since c | ab, so c divides ab.
Similarly, c | vbc
Hence c | uab + vbc
c | b. because b = uab + vbc.

Link for playlists: