filmov
tv
Calculus 2: how to NOT do partial fractions for the integrals (2 examples)
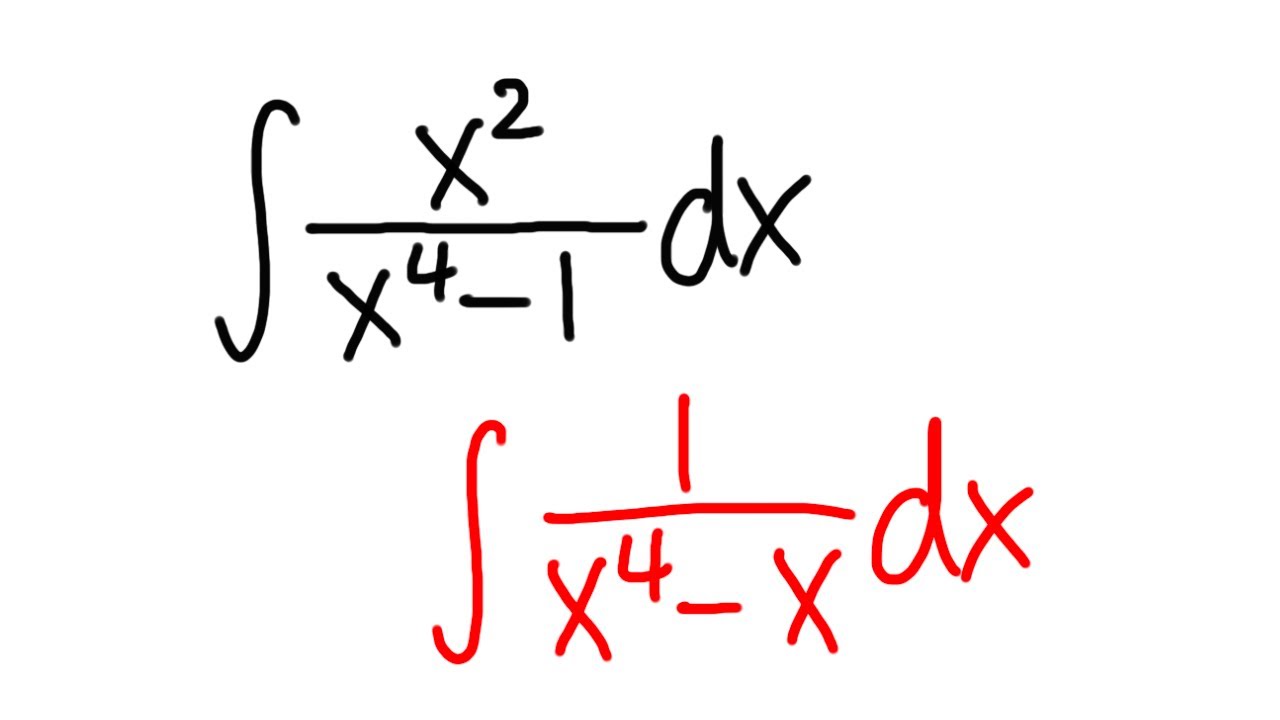
Показать описание
-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
Why People FAIL Calculus (Fix These 3 Things to Pass)
Calculus 2: how to NOT do partial fractions for the integrals (2 examples)
Stop Trying to Understand Math, Do THIS Instead
Calculus in a nutshell
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
ALL OF Calculus 2 in 5 minutes
The Hardest Calculus 2 Test I've Ever Given(Nobody got an A)
How REAL Men Integrate Functions
Ratio Test for Infinite Series Explained | Calculus 2
why calculus students struggle
the last question on my calc 2 final
What is the Hardest Calculus Course?
The 7 Levels of Math
Calculus 2 In Less Than 20 Minutes (Complete Overview Of Integral Calculus)
100 calculus 2 problems! (ultimate final exam review)
Work Problems | Calculus 2 Lesson 8 - JK Math
Calculus 2: The Fundamental Theorem of Calculus (...is not a theorem)
Monotonic Sequences and Bounded Sequences - Calculus 2
Convergence and Divergence - Introduction to Series
Calculus 2 - Basic Integration
The essence of calculus
Understand Calculus in 35 Minutes
Calculus 2 Lecture 9.1: Convergence and Divergence of Sequences
Calculus 2: Sequences (Section 11.1) | Math with Professor V
Комментарии
 0:03:15
0:03:15
 0:05:48
0:05:48
 0:05:21
0:05:21
 0:03:01
0:03:01
 0:22:40
0:22:40
 0:06:09
0:06:09
 0:07:06
0:07:06
 0:00:35
0:00:35
 0:12:05
0:12:05
 0:00:09
0:00:09
 0:08:51
0:08:51
 0:01:44
0:01:44
 0:08:44
0:08:44
 0:19:35
0:19:35
 7:17:57
7:17:57
 0:57:10
0:57:10
 0:29:42
0:29:42
 0:31:23
0:31:23
 0:16:18
0:16:18
 0:26:12
0:26:12
 0:17:05
0:17:05
 0:36:22
0:36:22
 2:27:29
2:27:29
 0:39:19
0:39:19