filmov
tv
How to use the difference of two squares to evaluate the limit by substitution
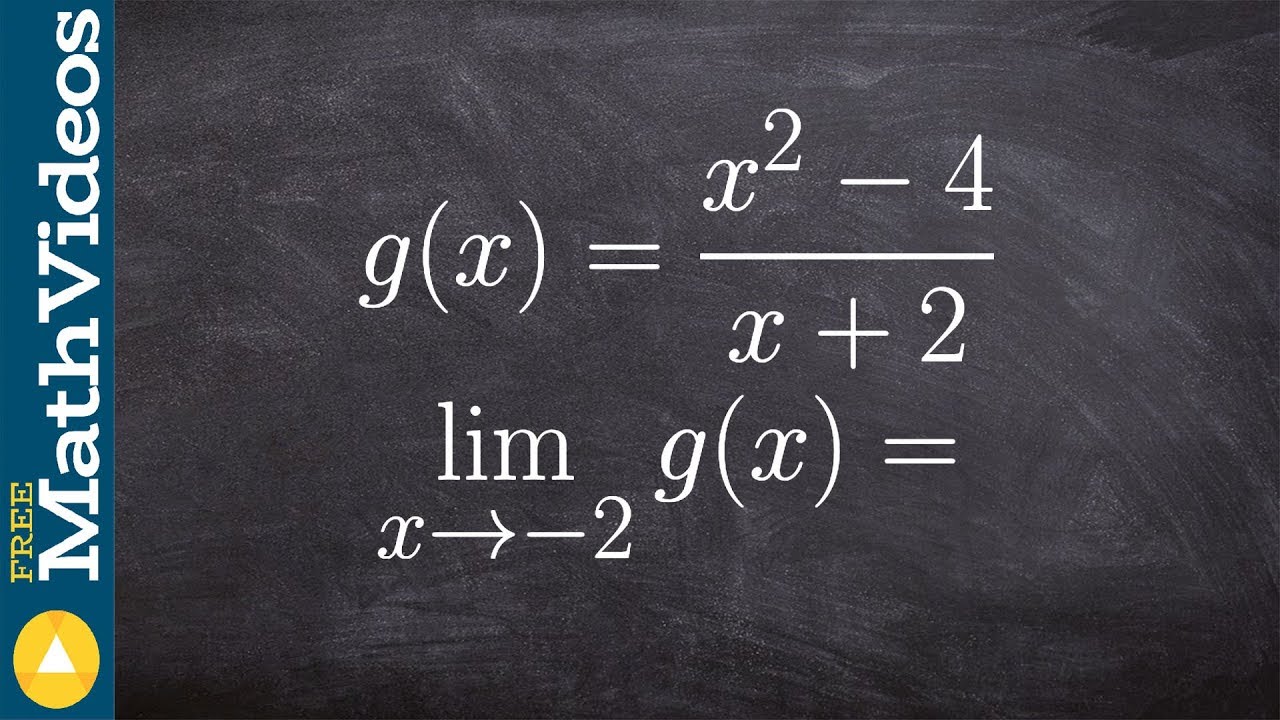
Показать описание
👉 Learn how to evaluate the limit of a function involving rational expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time.
The limit of a function is usually evaluated by direct substitution of the value which the variable tends to. When the function is a rational expression such that direct substitution leads to zero in the denominator, we find a way to either eliminate the denominator by multiplying both the numerator and the denominator by a common factor or decompose the denominator and the numerator into constituent parts so that like terms can cancel out.
Organized Videos:
✅The Limit
✅Evaluate Limits of Complex Fractions
✅Evaluate Limits of Polynomials
✅Evaluate Limits of Rational Expressions
✅Evaluate Limits with Square Roots
✅Evaluate Limits with Trig
✅Limits of Piecewise Functions
✅Evaluate Limits with Transcendentals
✅Evaluate Limits Difference Quotient
✅Evaluate Limits from a Graph
✅Evaluate Limits of Absolute Value
✅Evaluate Limits of Square Root
✅Holes and Asymptotes of Rational Functions
✅Learn about Limits
✅Find the Value that makes the Function Continuous
✅Is the Functions Continuous or Not?
✅Evaluate Limits using a Table of Values
✅Evaluate Limits at Infinity
Connect with me:
The limit of a function is usually evaluated by direct substitution of the value which the variable tends to. When the function is a rational expression such that direct substitution leads to zero in the denominator, we find a way to either eliminate the denominator by multiplying both the numerator and the denominator by a common factor or decompose the denominator and the numerator into constituent parts so that like terms can cancel out.
Organized Videos:
✅The Limit
✅Evaluate Limits of Complex Fractions
✅Evaluate Limits of Polynomials
✅Evaluate Limits of Rational Expressions
✅Evaluate Limits with Square Roots
✅Evaluate Limits with Trig
✅Limits of Piecewise Functions
✅Evaluate Limits with Transcendentals
✅Evaluate Limits Difference Quotient
✅Evaluate Limits from a Graph
✅Evaluate Limits of Absolute Value
✅Evaluate Limits of Square Root
✅Holes and Asymptotes of Rational Functions
✅Learn about Limits
✅Find the Value that makes the Function Continuous
✅Is the Functions Continuous or Not?
✅Evaluate Limits using a Table of Values
✅Evaluate Limits at Infinity
Connect with me:
 0:13:09
0:13:09
 0:04:40
0:04:40
 0:07:52
0:07:52
 0:00:54
0:00:54
 0:02:19
0:02:19
 0:01:17
0:01:17
 0:04:11
0:04:11
 0:06:06
0:06:06
 0:00:55
0:00:55
 0:02:28
0:02:28
 0:05:43
0:05:43
 0:15:33
0:15:33
 0:01:00
0:01:00
 0:20:18
0:20:18
 0:06:14
0:06:14
 0:06:24
0:06:24
 0:03:51
0:03:51
 0:08:19
0:08:19
 0:06:15
0:06:15
 0:01:00
0:01:00
 0:03:19
0:03:19
 0:13:21
0:13:21
 0:13:46
0:13:46
 0:10:21
0:10:21