filmov
tv
The Multiplicative Group of a Finite Field is Cyclic (Algebra 2: Lecture 11 Video 2)

Показать описание
Lecture 11: We started this lecture by discussing quotients of F[x]. We saw that the maximal ideals in F[x] are exactly the ideals (f(x)) generated by irreducible polynomials f(x). We then saw how to understand the structure of F[x]/(g(x)) in terms of the factorization of g(x). This was an application of the Chinese Remainder Theorem. We then built on a result from the previous lecture to show that a polynomial of degree d in F[x] can have at most d roots in F[x], even when roots are counted with multiplicity. We used this to prove that a finite subgroup of the multiplicative group of a field is cyclic. We gave two proofs of this result. We then showed how to use this result to understand the structure of the group of units of Z/nZ.
 0:06:30
0:06:30
 0:11:14
0:11:14
 0:13:40
0:13:40
 0:06:20
0:06:20
 0:11:17
0:11:17
 0:11:20
0:11:20
 0:22:10
0:22:10
 0:15:25
0:15:25
 0:01:42
0:01:42
 0:09:50
0:09:50
 0:02:08
0:02:08
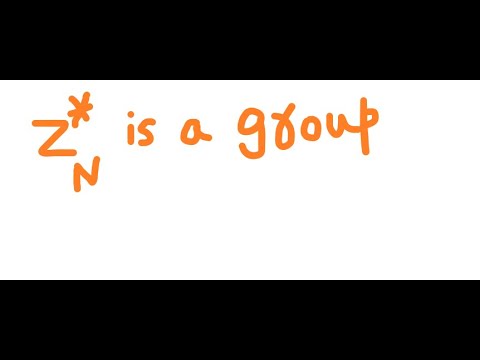 0:07:34
0:07:34
 0:04:21
0:04:21
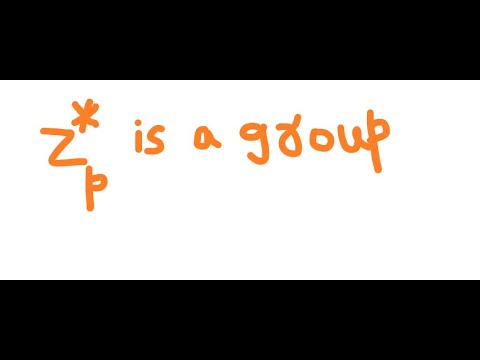 0:06:43
0:06:43
 0:01:45
0:01:45
 0:06:23
0:06:23
 0:10:38
0:10:38
 0:04:57
0:04:57
 0:04:14
0:04:14
 0:08:13
0:08:13
 0:12:27
0:12:27
 0:10:00
0:10:00
 0:20:36
0:20:36
 0:09:31
0:09:31