filmov
tv
Gauss Elimination Code - ANY SIZE - Python Code
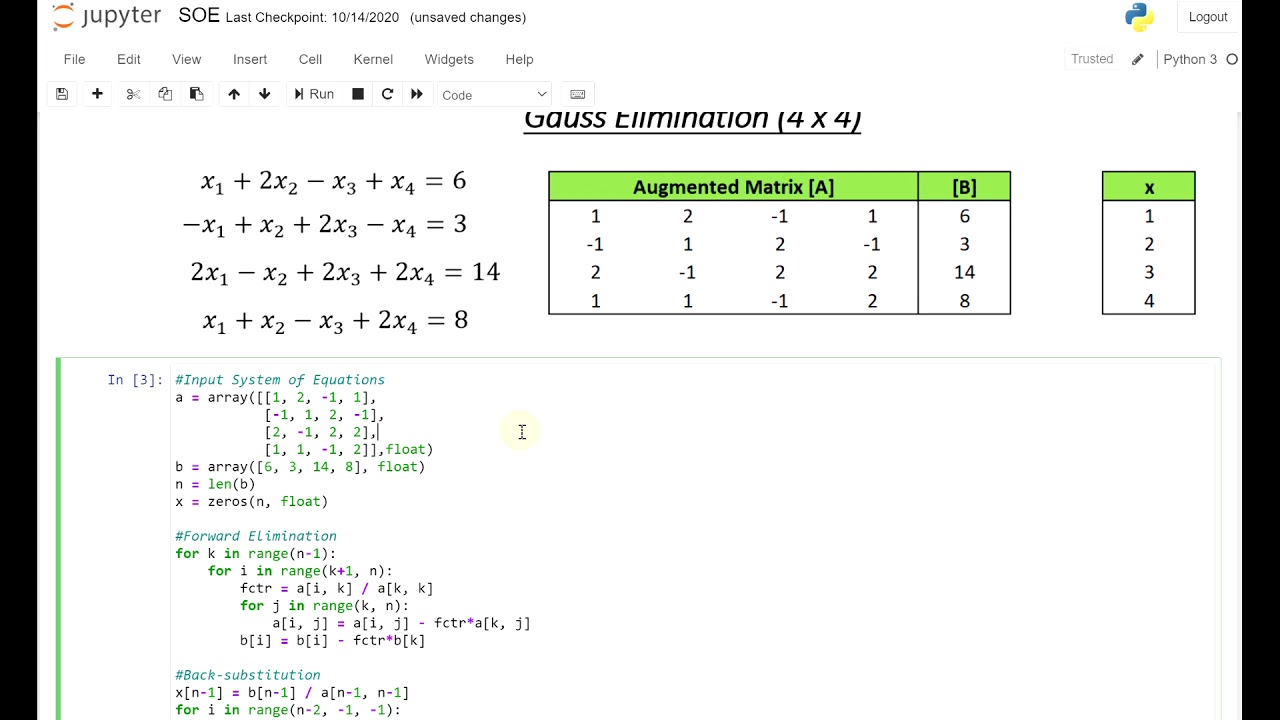
Показать описание
Gauss Elimination Code - ANY SIZE - Python Code
Gaussian Elimination In Python | Numerical Methods
Gauss Elimination - Simple MATLAB CODE/ PROGRAMMING
Gauss Elimination Explained with a C++ Program- (Tutorial)
gauss elimination method MATLAB code
Gauss Elimination Method with MATLAB code
GAUSS ELIMINATION IN C || C PROGRAMMING TUTORIALS
GAUSS-ELIMINATION METHOD CODE
Gaussian Elimination
Gaussian Elimination Python Program (AP CSP)
❤︎² Gaussian Elimination.. How? (mathbff)
Gauss Elimination Method - Working Example with C Program | Numerical Method | Dilip Kumar Gangwar
Gaussian Elimination - Demonstration
The Gauss Elimination Algorithm (ChEn 263 - Lecture 11)
Gauss Elimination Method | MATLAB Code
C++ Program For Gaussian Elimination
7.2: Matrices - Gauss elimination - 1
Gauss–Jordan elimination result only (using system of linear equation) in casio fx 991ES Calculator...
Example of Gaussian Elimination program in JS.
Gauss Elimination & Curve Fitting: Python Code Tutorial!
Gauss Elimination Method Tutorial - Part 1: Basic Procedure | Numerical Methods with Python
Implementing Gaussian Elimination in Scala
Gauss Elimination Code - EXCEL/VBA
Gauss Elimination With Partial Pivoting Example | Numerical Methods
Комментарии
 0:06:52
0:06:52
 0:12:01
0:12:01
 0:07:15
0:07:15
 0:23:55
0:23:55
 0:00:10
0:00:10
 0:25:00
0:25:00
 0:19:16
0:19:16
 0:09:11
0:09:11
 0:21:16
0:21:16
 0:00:59
0:00:59
 0:09:54
0:09:54
 0:49:39
0:49:39
 0:20:55
0:20:55
 0:42:16
0:42:16
 0:16:32
0:16:32
 0:06:59
0:06:59
 0:09:24
0:09:24
 0:02:07
0:02:07
 0:02:33
0:02:33
 0:04:56
0:04:56
 0:25:02
0:25:02
 0:17:11
0:17:11
 0:13:05
0:13:05
 0:05:36
0:05:36