Iterative Circle Projections, Chaos And Harmony

New research about a dynamic system which evolves via very simple rules involving a circle and some lines. We use projective geometry to investigate the different periodic orbits this system can have, and to reveal other perspectives of the dynamics.

We examine the the dynamics of a process involving a baseline and a circle. A sequence of points is created from simple projections. The next circle point is generated by drawing a tangent down from the current circle point to the baseline, and then linking this position on the baseline, with the previous circle point in the sequence, using another line.The other, new, circle point on this line is then taken to be the newly generated point.

Our findings from using projective geometry apply to more general cases, where the circle is replaced by another conic. Also, our results still hold true in various types on non-euclidean geometry.In addition to this 'projective perspective' we also examine the problem from a more concrete angle, and we treat it as if it occurs in the standard Euclidean plane. In this case, a classical circle parameterization method allows us to gain an explicit formula, which describes how new circle points are generated from old.

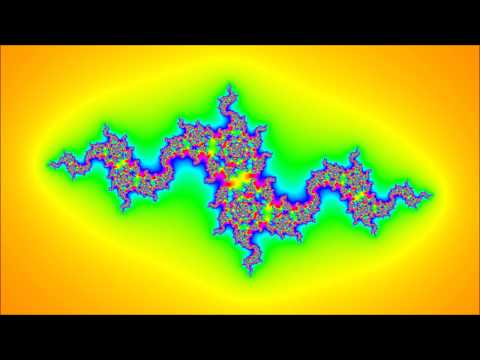
By looking at the process as a discrete dynamical system, we can picture the global dynamics. We note the appearance of intricate fractals that suggest these dynamics are sometimes chaotic. We also explore the notion of using these kind of system dynamics to design and program walking machines, made out of simple pieces, but potentially complex dynamics.

you can see the other orbits and much more info about the iterative circle projections by downloading the manuscript on it, from

link is near the bottom of the page

[hedronsciences]

very well done richard. Great. YMB. the quadrangle with only P1 and P2 is a real beauty and the only one that shows that shape. al others follow coxeter's notation. (more or les, as discussed) where the points of the diagonals with G are located between P1 and P2 as intersection of the `parallels´ of the edges of the quadrangle. did you find a 5-angle and up too?