filmov
tv
Solving a Diophantine System with Three Variables

Показать описание
This video is about solving a Diophantine System
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE:
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE:
Solving a Diophantine System
Solving a Diophantine System with Three Variables
Diophantine Equations! Can You Solve this System? | Simple & In-Depth Explanation
Solving A Diophantine Equation with Prime Numbers
I Solved A Diophantine System | Integers
A system of diophantine equations | feat. Fermat's Last Theorem | must watch till the end
Solving a Diophantine System | #integers
Solve Diophantine Equations by Factoring
Solving a Diophantine Equation by Factoring | Solve for Integer Solutions #NumberTheory
Solving a Diophantine Equation for Rational Solutions
A Linear Diophantine Equation
Let's Solve A Nice Diophantine System | New Year
Solving A Nice Diophantine Equation from Romania
A Diophantine Equation | x^2-y^2=23
Solving a Diophantine System with Three Variables
A Diophantine Equation | a^2=b^2+13
A Radical Diophantine Equation | #math #numbertheory
A Great Book on Diophantine Equations
A Nice System of Diophantine Equations | Math Olympiad
A Diophantine Equation | x^y=y^x
A Diophantine Equation with Integer Solutions
Can you solve this Systems of Diophantine Equations? 𝑥𝑦+𝑦𝑧=63 and 𝑥𝑧 + 𝑦𝑧 = 23...
5 simple unsolvable equations
Solving Linear Diophantine Equation
Комментарии
 0:07:00
0:07:00
 0:14:26
0:14:26
 0:12:14
0:12:14
 0:00:54
0:00:54
 0:08:10
0:08:10
 0:02:25
0:02:25
 0:07:00
0:07:00
 0:01:58
0:01:58
 0:07:08
0:07:08
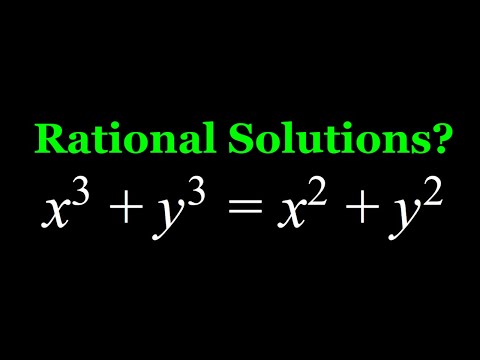 0:07:31
0:07:31
 0:00:27
0:00:27
 0:08:53
0:08:53
 0:09:09
0:09:09
 0:00:55
0:00:55
 0:14:26
0:14:26
 0:00:46
0:00:46
 0:00:28
0:00:28
 0:00:18
0:00:18
 0:11:01
0:11:01
 0:00:56
0:00:56
 0:00:49
0:00:49
 0:03:33
0:03:33
 0:00:50
0:00:50
 0:11:16
0:11:16