REGRA DE SARRUS

Olá amigos do meu canal no YouTube.
Este é um vídeo sobre a Regra de Sarrus.
- Professor, para que que serve essa regra?
Meus amigos, essa regra serve para que a gente possa calcular o determinante de uma matriz quadrada de ordem 3, isto é, uma matriz com 3 linhas e 3 colunas.
É o tipo de determinante que nós temos aqui.
- Ok, professor. E como é que a Regra de Sarrus funciona?
Primeiro, repetimos as duas primeiras colunas, após a última, do lado direito.
Depois, realizamos algumas multiplicações da seguinte forma.
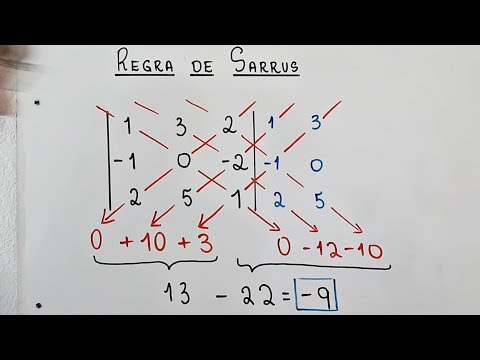
Calculamos o produto dos elementos da diagonal principal e anotamos o resultado. Veja:
1*0*1=0
Agora, avançamos paralelamente à diagonal principal e realizamos a multiplicação desses números. Veja:
3*(-2)*2=-12
Agora, avançamos mais uma vez paralelamente à diagonal principal e realizamos a multiplicação desses números. Veja:
2*(-1)*5=-10
Pronto, terminamos essa parte.
Vamos considerar, dessa vez, os elementos da diagonal secundária para começar.
2*0*2=0
Quando realizamos a multiplicação dos elementos da diagonal secundária e também das paralelas a ela, devemos ter o cuidado de registrar sempre o oposto do produto que obtemos. Neste caso, o oposto de 0 é 0 mesmo e então apenas anotamos o seu valor. Fique atento para o que faremos mais adiante.
Caminhando, paralelamente à diagonal secundária, agora, temos:
1*(-2)*5=-10
Devemos registrar o oposto desse valor, ou seja, escrevemos +10.
Finalmente, temos:
3*(-1)*1=-3
Seguindo a regra, escrevemos o oposto desse valor, isto é, +3.
Para finalizar, basta realizar a adição de todos esses valores. Assim, temos:
0+10+3=13
0-12-10=-22
13-22=-9
Conclusão: o valor do determinante é -9.

Segunda parte do nosso vídeo!
Agora, você tentar calcular esse determinante e verificar se aprendeu a Regra de Sarrus.
Mas antes, não esqueça de clicar em gostei e deixar um comentário sobre este vídeo.
Tentou resolver? Eu espero que sim.
Vamos partir para uma resolução!
Repetimos as duas primeiras colunas após a última, na direita.
Calculamos o produto dos elementos da diagonal principal:
(-3)*1*2=-6
Caminhando paralelamente à diagonal principal, temos:
1*(-3)*5=-15
Mais uma vez, temos:
7*2*4=+56
Essa etapa acabou, vamos partir para a diagonal secundária.
Agora, devemos tomar sempre o oposto do produto que calcularmos.
Veja:
7*1*5=35
E escrevemos -35
Agora,
(-3)*(-3)*4 =36
E escrevemos -36, sempre o oposto.
Finalmente,
1*2*2=4
Mas escrevemos -4.
Essa parte acabou.
Só o que nos resta fazer é realizar a adição de todos esses valores.
Vou repetir aqui o -35 e em vez de -36-4, vou escrever logo -40.
Como -6-15 é -21, aqui ficamos com -21+56.
-35-40 é igual a -75.
Agora, -21+56=35, positivo.
Fica a dica: se você está com dificuldade neste departamento, então precisa estudar adição com números inteiros.
Finalmente, -75+35 é igual a -40.
Conclusão: o valor do determinante é -40.
Acho que não precisa nem dizer: se este vídeo te ajudou, é provável que o conteúdo deste canal seja útil para você. Dessa forma, inscreva-se e venha fazer parte da nossa sala de aula virtual.
Um abraço e até a próxima, tchau!

Música de fundo:

[mcrisstchornobay]

um vídeo de 2017 salvando meu ano letivo em 2021... MUITO OBRIGADA

[pedrocassenote]

muito boa esta aula, o senhor explica claramente e com muita paciência, ajudando no aprendizado.
deixei meu like.

[cindylauper]

“nem doeu” eu ri Parabéns, explica muito bem 👏🏼 Me salvou

[noealexandre]

Eu sou Angolano estás de parabéns o seu vídeo tem me ajudado muito na resolução desses exercícios.

[alissonprazeres]

muito bom, com o passar do tempo vamos esquecendo oq aprendemos na escola, e quando queremos fazer algum concurso ou um vestibular, varios professores explicam de forma diferente da qual eu aprendi(macetes), mas esse vídeo me fez lembrar de tudo q aprendi na escola, me salvou, obrigado!

[robertguilherme]

Vc conseguiu de uma forma rápida e precisa, ensinar esse conteúdo.
Obrigado por compartilhar seus conhecimentos com todos aqueles q querem reter pra si, esse conteúdo, matemático.

[gustavoluizalves]

Olha... sem palavras. Meu desespero tava muito grande e eu não sabia de nada, mas como DEUS é maravilhoso, existe esse vídeo e essa pessoa maravilhosa que tem realmente o dom de ensinar. Meus parabéns professor!!!

#pormaisprofessoresassim

[nahumrodrigues]

Muito legal a forma que você fez esse vídeo. Mesmo sabendo o assunto, é bem bacana assistir.

[jamillycampos]

O único no YouTube que realmente explicou bem e eu entendi e aprendi muuuito🥰 obrigada sério!

[parkinho.]

Me salvou professor, muito obrigado🤝🤝

[viniciusaugusto]

Rápida, clara, direta e bem explicativa. Excelente aula!!👏🏼👏🏼

[helenferreiraferreira]

a melhor ate agora, com muita facilidade, bom demais!

[brunodomingues]

ME AJUDOU DEMAIS! só estou com um probleminha nos sinais porém ME AJUDOU MUITO!

[kayakihaki]

Um bagulho simples ...
As outras vídeo aula tem 10-15min pra explicar tanto e quem ta vendo n entender nd, , vc falou de uma maneira resumida e fácil de entender ... gostei d+, +1 inscrito

[marcelolopespb]

Simples e objetivo. Além do mais, você pediu para que fizéssemos a outra questão para ver se realmente aprendemos e consegui fazer. Amo esse método de ensino. Parabéns.

[MariaDasDores-joup]

Professor! Muito obgh!.
Que Deus could continue abencoando o senhor, cada vez mais...
Continue assim... Ensinando oque vç aprendeus de melhor...
Parabens!

[jeovavieirafernandes]

Sem dúvidas a melhor explicação que eu tive a oportunidade de assistir

[mariaveraluciaalvesvera]

👏👏Gostei muito da aula ensina muito bem.

[tuliobolo]

Conheci seu canal hoje enquanto procurava resoluções de algumas questões do ITA, vestibular que pretendo prestar no ano que vem pela primeira vez. E devo dizer que Eu procurava o tipo de conteúdo que você trás há muito tempo. Espero que continue com o canal, muito obrigado!! :)

[raqueldames]

Gostei muito dessa explicação, Obrigada😊