filmov
tv
Can you solve this If x^2+x+1=0 then Find x^1999+x^2000=? | Olympiad Math Question!
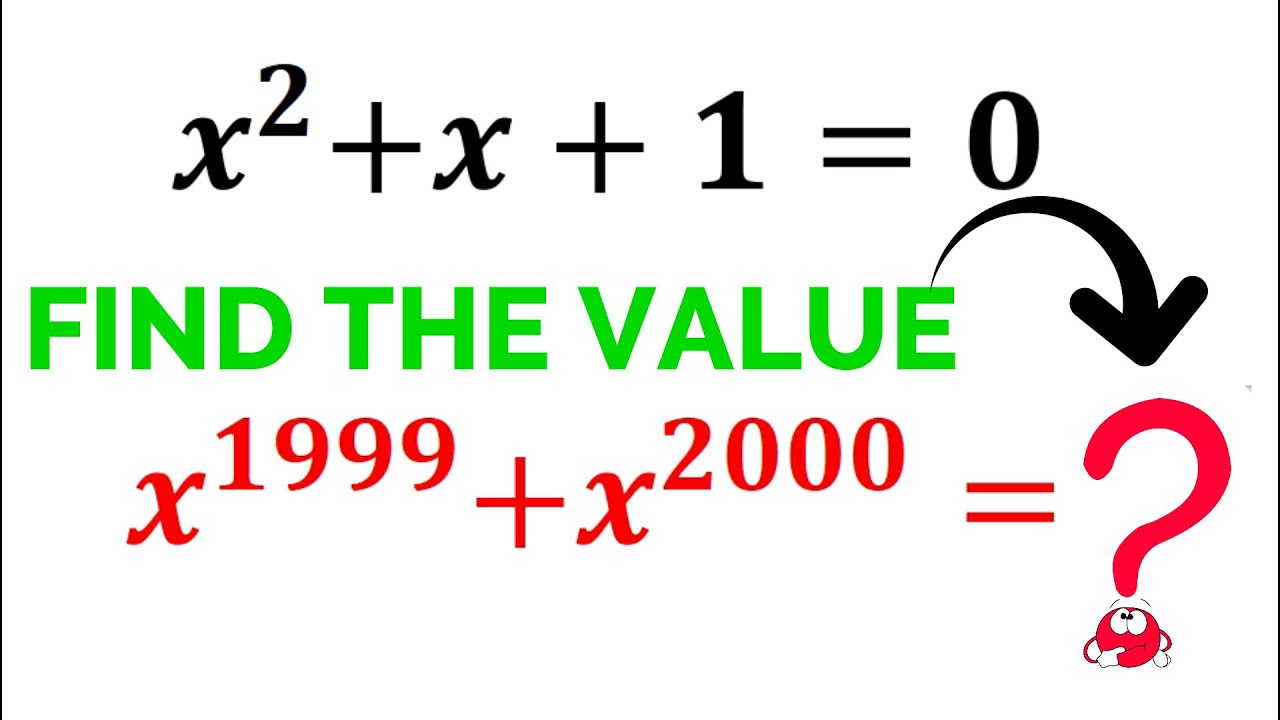
Показать описание
Can you solve this If x^2+x+1=0 then Find x^1999+x^2000=? | Olympiad Math Question!
#challengingmathproblem #matholympiad
#challengingmathproblem #matholympiad
Can A Crow Solve 9 Impossible Puzzles?
Can you solve the three gods riddle? - Alex Gendler
Can you solve the prisoner hat riddle? - Alex Gendler
Can you solve the wizard standoff riddle? - Dan Finkel
Can you solve the bridge riddle? - Alex Gendler
How fast can you solve a Rubik’s Cube?? 🤔
Can you solve the famously difficult green-eyed logic puzzle? - Alex Gendler
Can a Robot solve this...?
Can You Solve These Tricky Riddles? Part 2 #quiz #riddles #shorts
Can you solve the jail break riddle? - Dan Finkel
If You Solve These 20 Riddles, Google Should Hire You
Can you solve the Alice in Wonderland riddle? - Alex Gendler
Can you solve the egg drop riddle? - Yossi Elran
Can you solve this cube? 🤔
Can you solve the locker riddle? - Lisa Winer
If You Solve 10% of These Riddles, You Are Better Than Sherlock
Can you solve the troll’s paradox riddle? - Dan Finkel
Even the Smartest Professor Can't Solve All 17 Riddles
Can you solve the birthday cake riddle? - Marie Brodsky
Can you solve a 2 move Rubik’s cube scramble? 🤔
Can you solve this puzzle?
Can you solve the alien probe riddle? - Dan Finkel
Can you solve the time travel riddle? - Dan Finkel
Can you solve this exam question from India?
Комментарии
 0:23:20
0:23:20
 0:04:54
0:04:54
 0:04:35
0:04:35
 0:05:26
0:05:26
 0:03:50
0:03:50
 0:00:18
0:00:18
 0:04:42
0:04:42
 0:00:20
0:00:20
 0:01:00
0:01:00
 0:03:25
0:03:25
 0:12:33
0:12:33
 0:05:05
0:05:05
 0:04:47
0:04:47
 0:01:49
0:01:49
 0:03:50
0:03:50
 0:10:48
0:10:48
 0:03:45
0:03:45
 0:12:23
0:12:23
 0:04:48
0:04:48
 0:00:24
0:00:24
 0:00:55
0:00:55
 0:05:09
0:05:09
 0:04:32
0:04:32
 0:06:37
0:06:37