New Density Matrix Renormalization Group-based Methods for Molecular Simulations

New Density Matrix Renormalization Group-based Methods for Molecular Simulations

Alberto Baiardi, Markus Reiher

The full configuration interaction (full CI) method represents the election algorithm for exact molecular simulations. However, its high computational cost makes it applicable only to small molecular systems. This prohibitive scaling can be tamed with tensor-based compression
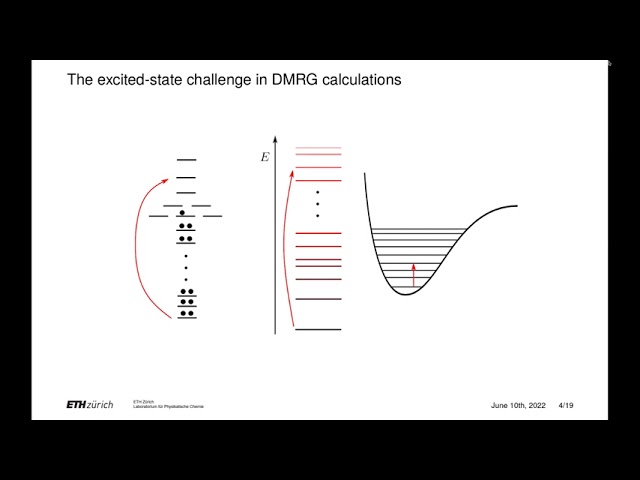
schemes, such as the density matrix renormalization group (DMRG). 1 To date, DMRG has been mostly applied to electronic problems. In this talk we will describe DMRG-based methods for studying three new classes of molecular simulations. 1 We will first introduce DMRG-based algorithms for simulating vibrational spectra both within2–5 and beyond6,7 the Born-Oppenheimer approximation. We will then introduce the time-dependent DMRG method to simulate nonequilibrium phenomena in complex molecular systems. 8,9 Finally, we will introduce an explicitlycorrelated DMRG variant that relies on the transcorrelated approach. 10,11 We will show the reliability of all these methods, which we implemented in the QCMaquis module of OpenMolcas,12 by comparing their accuracy with alternative state-of-the-art approaches.

References
[1] Baiardi, A.; Reiher, M. The density matrix renormalization group in chemistry and molecular physics: Recent developments and new challenges. J. Chem. Phys. 2020, 152, 040903.
[2] Baiardi, A.; Stein, C. J.; Barone, V.; Reiher, M. Vibrational Density Matrix Renormalization Group. J. Chem. Theory Comput. 2017, 13, 3764–3777.
[3] Baiardi, A.; Stein, C. J.; Barone, V.; Reiher, M. Optimization of highly excited matrix product states with an application to vibrational spectroscopy. J. Chem. Phys. 2019, 150, 094113.
[4] Glaser, N.; Baiardi, A.; Reiher, M. Tensor Network States for Vibrational Spectroscopy. ArXiv e-prints 2021, 2109.08961.
[5] Baiardi, A.; Kelemen, A. K.; Reiher, M. Excited-state DMRG made simple with FEAST. J. Chem. Theory Comput. 2021, 18, 430.
[6] Muolo, A.; Baiardi, A.; Feldmann, R.; Reiher, M. Nuclear-electronic all-particle density matrix renormalization group. J. Chem. Phys. 2020, 152, 204103.
[7] Feldmann, R.; Muolo, A.; Baiardi, A.; Reiher, M. Quantum Proton Effects from Density Matrix Renormalization Group Calculations. J. Chem. Theory Comput. 2022, 18, 250.
[8] Baiardi, A.; Reiher, M. Large-scale quantum-dynamics with matrix product states. J. Chem. Theory Comput. 2019, 15, 3481–3498.
[9] Baiardi, A. Electron Dynamics with the Time-Dependent Density Matrix Renormalization Group. J. Chem. Theory Comput. 2021, 17, 3320–3334.
[10] Baiardi, A.; Reiher, M. Transcorrelated density matrix renormalization group. J. Chem. Phys. 2020, 153, 164115.
[11] Baiardi, A.; Lesiuk, M.; Reiher, M. Explicitly correlated electronic structure calculations with transcorrelated matrix product operators. ArXiv e-prints 2022,