filmov
tv
The Schrodinger Equation is (Almost) Impossible to Solve.

Показать описание
Sure, the equation is easily solvable for perfect / idealized systems, but almost impossible for any real systems.
The Schrodinger equation is the governing equation of quantum mechanics, and determines the relationship between a system, its surroundings, and a system's wave function.
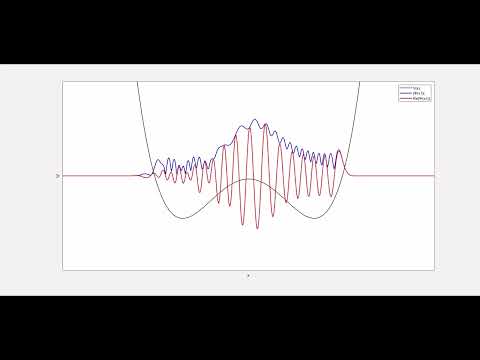
The wave function contains all the information we can know about a system, such as the probabilities of finding a particle within the system in different regions of space. Specifically, the square modulus of the wave function is related to any measurement probability.
The Schrodinger equation simplifies down to "kinetic energy + potential energy = total energy", but using the language and quantities defined by the theory of quantum mechanics.
We can set up the Schrodinger equation for any system that we are studying, simply by adding together all the kinetic energies and potential energies within the system. In this video, we see how to do that for a hydrogen atom and a helium atom. Then we "solve" the Schrodinger equation by finding the allowed wave functions.
With a hydrogen atom, we merely need to account for the potential energy that comes about due to the electron-proton interaction. Since they are both charged particles, they exert electrostatic forces on each other, and hence there is a potential energy between them.
In a helium atom (2 protons, 2 neutrons, 2 electrons), things become a bit more complicated. To make things simple, we make 3 assumptions: (1) the nucleus is stationary, since it's much more massive than the electrons, (2) the nucleus behaves as one single object in order to avoid accounting for the interactions between the particles making up the nucleus, and (3) the atom is isolated and does not interact with anything outside it.
These simplifications allow us to much more easily build the Schrodinger equation for our helium atom. We only need to account for the kinetic energies of the electrons since we assume the nucleus is stationary. We also only need to account for 3 sources of potential energy. Two of these are the interactions between the nucleus and the two electrons, and the third is the electron-electron interaction. We would have account for many more terms if we did not use the simplifications outlined above.
At this point, we have a differential equation that we can solve in order to find the allowed wave functions. But this equation is extremely difficult to solve analytically, and we don't have many techniques to do it. We instead have to resort to further simplifications or the use of computers to find "brute force" solutions. This last method is basically trial and error but with fairly educated guesses.
Thanks for watching, please do check out my socials here:
Instagram - @parthvlogs
Music Chanel - Parth G's Shenanigans
Here are some affiliate links for things I use! I make a small commission if you make a purchase through these links.
Cards linked in this video:
Timestamps:
0:00 - What Does the Schrodinger Equation Mean, and How Do We Solve It?
3:29 - Building the Schrodinger Equation for the Hydrogen Atom
5:05 - A Simplified Model of the Helium Atom
7:06 - Building the Schrodinger Equation for a Simplified Helium Atom
10:07 - Solving the Schrodinger Equation?
The Schrodinger equation is the governing equation of quantum mechanics, and determines the relationship between a system, its surroundings, and a system's wave function.
The wave function contains all the information we can know about a system, such as the probabilities of finding a particle within the system in different regions of space. Specifically, the square modulus of the wave function is related to any measurement probability.
The Schrodinger equation simplifies down to "kinetic energy + potential energy = total energy", but using the language and quantities defined by the theory of quantum mechanics.
We can set up the Schrodinger equation for any system that we are studying, simply by adding together all the kinetic energies and potential energies within the system. In this video, we see how to do that for a hydrogen atom and a helium atom. Then we "solve" the Schrodinger equation by finding the allowed wave functions.
With a hydrogen atom, we merely need to account for the potential energy that comes about due to the electron-proton interaction. Since they are both charged particles, they exert electrostatic forces on each other, and hence there is a potential energy between them.
In a helium atom (2 protons, 2 neutrons, 2 electrons), things become a bit more complicated. To make things simple, we make 3 assumptions: (1) the nucleus is stationary, since it's much more massive than the electrons, (2) the nucleus behaves as one single object in order to avoid accounting for the interactions between the particles making up the nucleus, and (3) the atom is isolated and does not interact with anything outside it.
These simplifications allow us to much more easily build the Schrodinger equation for our helium atom. We only need to account for the kinetic energies of the electrons since we assume the nucleus is stationary. We also only need to account for 3 sources of potential energy. Two of these are the interactions between the nucleus and the two electrons, and the third is the electron-electron interaction. We would have account for many more terms if we did not use the simplifications outlined above.
At this point, we have a differential equation that we can solve in order to find the allowed wave functions. But this equation is extremely difficult to solve analytically, and we don't have many techniques to do it. We instead have to resort to further simplifications or the use of computers to find "brute force" solutions. This last method is basically trial and error but with fairly educated guesses.
Thanks for watching, please do check out my socials here:
Instagram - @parthvlogs
Music Chanel - Parth G's Shenanigans
Here are some affiliate links for things I use! I make a small commission if you make a purchase through these links.
Cards linked in this video:
Timestamps:
0:00 - What Does the Schrodinger Equation Mean, and How Do We Solve It?
3:29 - Building the Schrodinger Equation for the Hydrogen Atom
5:05 - A Simplified Model of the Helium Atom
7:06 - Building the Schrodinger Equation for a Simplified Helium Atom
10:07 - Solving the Schrodinger Equation?
Комментарии
 0:14:08
0:14:08
 0:01:37
0:01:37
 0:16:43
0:16:43
 0:49:30
0:49:30
 0:29:55
0:29:55
 0:17:09
0:17:09
 1:27:34
1:27:34
 0:13:04
0:13:04
 0:09:47
0:09:47
 0:01:31
0:01:31
 0:53:20
0:53:20
 0:12:19
0:12:19
 0:12:57
0:12:57
 0:07:23
0:07:23
 0:09:13
0:09:13
 0:01:01
0:01:01
 0:07:41
0:07:41
 0:00:58
0:00:58
 0:01:26
0:01:26
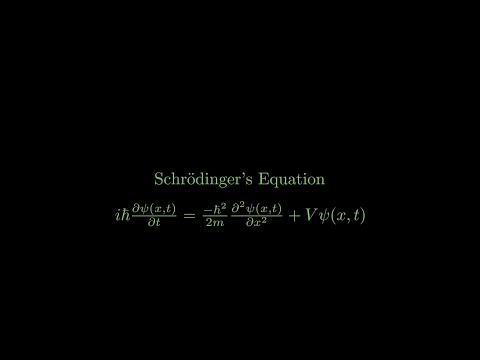 0:33:23
0:33:23
 0:12:41
0:12:41
 0:22:08
0:22:08
 0:04:43
0:04:43
 0:52:02
0:52:02