filmov
tv
EDO de Bernoulli

Показать описание
EQUAÇÃO DIFERENCIAL DE BERNOULLI ➡️ EXEMPLO 1
Ecuaciones diferenciales | La ecuación de Bernoulli
62. Ecuación diferencial de Bernoulli. EJERCICIO RESUELTO
EDO de Bernoulli
🟣ECUACIÓN DIFERENCIAL DE BERNOULLI🟣 #mateciencias
►Aprende Fácil y Rápidamente la Ecuación Diferencial de Bernoulli
EDO DE BERNOULLI (TEORÍA) - ECUACIONES DIFERENCIALES
24 VIDEO DE LA CLASE PRESENCIAL DE LA EDO DE BERNOULLI
E D O de Bernoulli
E.D.O. De Bernoulli | Ejercicio De Práctica
EDO de Bernoulli. ejercicio v4
Ecuación de Bernoulli (Ecuaciones Diferenciales) Solución Completa
GRINGS - Equação Diferencial de Bernoulli - Análise Completa
EDO de Bernoulli
Considere la EDO de bernoulli: xy´- y^3*e^x - y= 0 despues de hacer el cambio de variables
EDO BERNOULLI| Ecuaciones DIFERENCIALES de BERNOULLI paso a paso
EDO - 17 - Equação de Bernoulli
EDO de Bernoulli
EDO: Bernoulli (ejemplos)
Edo de Bernoulli - Zill 2.6 - exercício 1
EDO de BERNOULLI - EXEMPLO
EJERCICIO EDO DE BERNOULLI - ECUACIONES DIFERENCIALES
07 Edo de Bernoulli | ecuaciones diferenciales
Ecuación de Bernoulli resuelta por Cambio de Variable
Комментарии
 0:10:53
0:10:53
 0:05:19
0:05:19
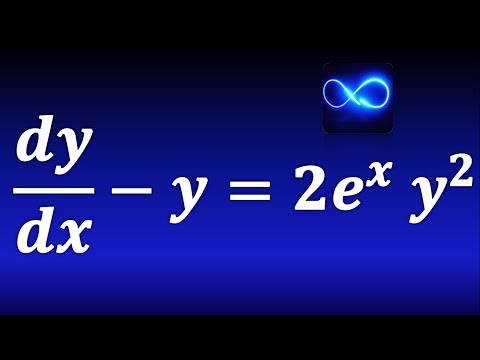 0:11:39
0:11:39
 0:07:01
0:07:01
 0:00:58
0:00:58
 0:12:57
0:12:57
 0:03:48
0:03:48
 0:08:57
0:08:57
 0:20:43
0:20:43
 0:15:16
0:15:16
 0:13:30
0:13:30
 0:10:52
0:10:52
 0:13:46
0:13:46
 0:16:30
0:16:30
 0:00:26
0:00:26
 0:04:10
0:04:10
 0:14:54
0:14:54
 0:09:42
0:09:42
 0:10:25
0:10:25
 0:23:15
0:23:15
 0:04:16
0:04:16
 0:12:37
0:12:37
 0:04:10
0:04:10
 0:11:33
0:11:33