filmov
tv
Intersection of 3 cylinders volume

Показать описание
In this video, I calculate the volume of the Steinmetz 3-solid obtained by intersecting three cylinders, using a symmetry argument and cylindrical coordinates. It’s actually not as bad as you think!
Intersection of 3 cylinders volume
VOLUME INTEGRATION | Intersection of 3 Cylinders
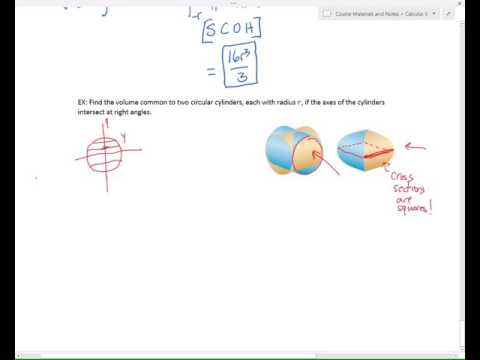
Calculus 2 - Volume of intersecting cylinders (Example)
Volume Intersection Three Cylinders
Volume of intersecting cylinders via triple integrals
Volume bounded by Cylinder and Planes Volume by Double Intgeral Higher Engineering Mathematics
Surface Area of Intersecting Cylinders Example
Triple Integrals in Cartesian Coordinates | Volume between Surfaces
Find the volume of the intersection of two cylinders using calculus
Find the volume of the intersection of the two cylinders via triple integrals
Volume of the Intersection of Two Cylinders
Intersection of 2 cylinders volume
48 3 Intersecting Cylinders
Unizor - Geometry3D - Cylinders - Easy Problems
Compare the volume of the two given cylinders !
Sketching the quadric surface (KristaKingMath)
Use a Triple Integral to Find the Volume Bounded by Two Paraboloid (Cylindrical)
Volume common to the Cylinders(Lecture-5)
Calculus 3 Lecture 11.6: Cylinders and Surfaces in 3-D
Three dimensional surfaces: cylinders
Calculus 9.6 Volume of the Intersection of Two Cylinders
Intersecting Cylinders
Calculus 3 Lecture 14.7: TRIPLE Integrals Over Regions with CYLINDRICAL or SPHERICAL Coord.
Volume of a bicylinder -- wait! What is a bicylinder?
Комментарии
 0:20:38
0:20:38
 0:10:39
0:10:39
 0:05:37
0:05:37
 0:05:39
0:05:39
 0:09:33
0:09:33
 0:06:24
0:06:24
 0:04:26
0:04:26
 0:07:13
0:07:13
 0:03:49
0:03:49
 0:10:21
0:10:21
 0:05:53
0:05:53
 0:13:35
0:13:35
 0:02:24
0:02:24
 0:34:32
0:34:32
 0:03:11
0:03:11
 0:08:05
0:08:05
 0:07:29
0:07:29
 0:06:54
0:06:54
 2:32:27
2:32:27
 0:06:29
0:06:29
 0:09:57
0:09:57
 0:10:17
0:10:17
 3:20:10
3:20:10
 0:10:18
0:10:18