Double Integration Method Example 2 (1/2) - Mechanics of Materials

This is a double integration method example problem for a simply supported beam with linear and uniform distributed loads. This video shows how to calculate slope and displacement functions and then determine the maximum displacement of the beam.

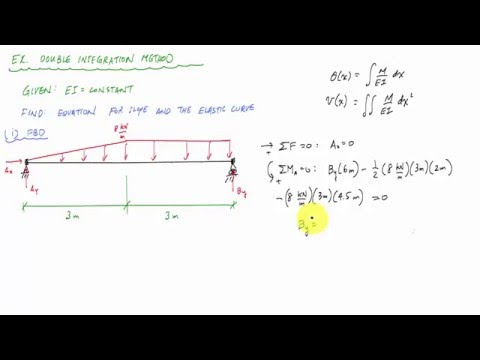
Part 1: Calculating Reactions, Moment Functions, and Antiderivatives

Part 2: Identifying boundary and continuity conditions, solving for constants, determining the maximum deflection of the beam

[ahmattahar]

Man your "welcome back to structure free definitively killed me lmao

[ahmattahar]

Reviewing basics is always a pleasure. Thanks

[waichingwong]

You have saved my final examination. Yeah~

[DrDerivative]

Is it possible to look at section 2 from the left. starting at the 3m mark (change from linear to constant)? Im attempting that way and I get that M2 = -4x^2. However im missing the + 22. How can i account for that using the technique i described in the sentance above?

[johaneswijaya]

Can we use singularity for this kind of question where the triangular distribution load ends at the center of the beam length?

[brookesmith]

thanks so so much for your perfectly clear, well paced, engaging vids. think I spotted in the expression for deflection with respect to x1,
should be -1/20 * x1^5 rather than -1/45 * x1^5

[stevearnold]

at time 4.22 x/3 should be 2x/3 ?.  The triangular load should act at a distance of 2x/3 or (x-x/3). ???