Supplemental Video: Power Series - finding a power series representation for f(x)=arctan(x)

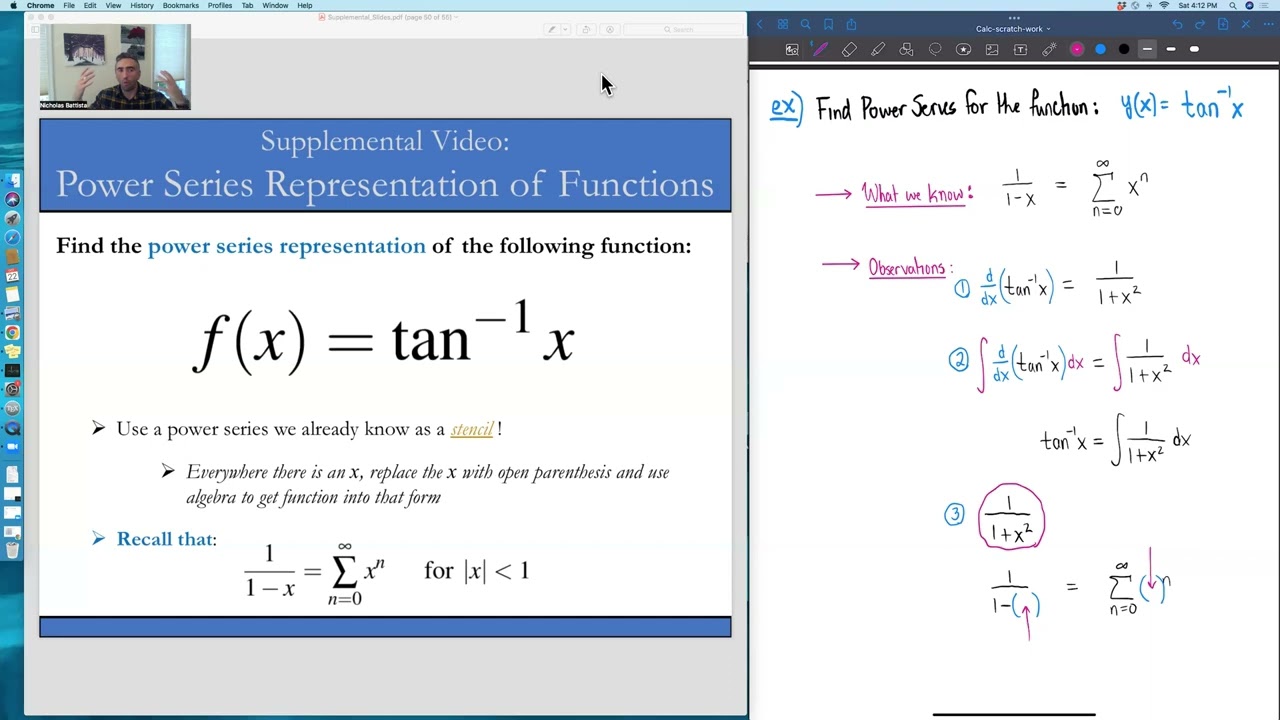
In this video, we find a power series representation for the function f(x)=arctan(x) by using information about a power series that we already know.

Power Series that will help us: 1/(1-x) = SUM_{n=0}^{infinity} x^n

Observations/Idea:
[1] The derivative of arctan(x) is 1/(1+x^2)
[2] The anti-derivative of 1/(1+x^2) = arctan(x) + C
[3] We can find a power series representation for 1/(1+x^2) and then integrate it!
[4] Can use composition of functions to give us new power series, i.e., make a "stencil" out of a power series that we know
[5] Use algebra to get function that we're given into the appropriate "stencil" form
[6] Substitute!